题目内容
有三根细木棒a，b，c，长分别为a=6cm，b=12cm，c=9cm，小臻想找一个细木棒d把它们相连，若d=28cm可以吗？如果不能，你能不能想想办法？怎样能使28cm木棒派上用场？（取整数长度）
考点：三角形三边关系
专题：
分析：由6+9+12=27＜28，得出d=28cm不能围成四边形，要想围成四边形长棒截短必须＜27cm，则最长为26cm，根据三角形三边关系定理即可求解．
解答：
解：∵6+9+12=27＜28，
∴不能围成成四边形．
可以将长棒截短必须＜27，则最长为26．
∵26-12=14，6+9＞14，
∴6、9、14可以围成△ABC，BC=14，AC=9．
平移AC到ED，D在BC延长线上，CD=12，BD=BC+CD=14+12=26．
即在四边形ABDE中，AB=6cm，BD=26cm，DE=9cm，EA=12cm．
解：∵6+9+12=27＜28，∴不能围成成四边形．
可以将长棒截短必须＜27，则最长为26．
∵26-12=14，6+9＞14，
∴6、9、14可以围成△ABC，BC=14，AC=9．
平移AC到ED，D在BC延长线上，CD=12，BD=BC+CD=14+12=26．
即在四边形ABDE中，AB=6cm，BD=26cm，DE=9cm，EA=12cm．
点评：本题考查了三角形三边关系定理：三角形两边之和大于第三边，三角形的两边之差小于第三边．
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图，已知l是第一、三象限的角平分线，点P与P′关于l对称，已知点P的坐标为（a，b），猜想P′的坐标是什么？并说明你猜想的正确性．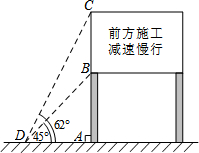
进入3月份，我市“两横三纵”快速路系统全线开工．为缓解市区内一些主要路段交通拥挤的现状，交警部门在一些主要路口设立了如图所示的交通路况显示牌．已知立杆AB的高度是3米，从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°．求路况显示牌BC的高度．（精确到0.1米）