题目内容
如果一个多边形的一个内角的外角与其内角的和为600°，则这个多边形的边数为 ．
考点：多边形内角与外角
专题：
分析：根据n边形的内角和定理可知：n边形内角和为（n-2）×180°．设这个外角度数为x度，利用方程即可求出答案．
解答：解：设这个外角度数为x，根据题意，得
（n-2）×180°+x=600°，
解得：x=600°-180°n+360°=960°-180°n，
由于0＜x＜180°，即0＜960°-180°n＜180°，
解得4
＜n＜5
，
所以n=5．
故这个多边形的边数为5．
故答案为：5．
（n-2）×180°+x=600°，
解得：x=600°-180°n+360°=960°-180°n，
由于0＜x＜180°，即0＜960°-180°n＜180°，
解得4
| 1 |
| 3 |
| 1 |
| 3 |
所以n=5．
故这个多边形的边数为5．
故答案为：5．
点评：主要考查了多边形的内角和定理．n边形的内角和为：180°•（n-2）．
练习册系列答案
相关题目
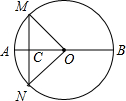如图，AB是⊙O的直径，MN是弦，且AB⊥MN，若AB=4，且∠MON=90°，则MC=
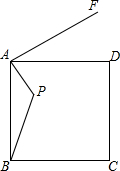已知点P是边长为5的正方形ABCD内一点，且AP=2，AF⊥AP，垂足是点A，若在射线AF上找一点M，使以点A，M，D为顶点的三角形与△ABP相似，则AM为
8个一样大小的长方形恰好拼成一个大的长方形（如图1），也可以拼如图2那样的正方形，但这个大正方形中间恰好留下了一个边长为2cm的小正方形．则每一个小长方形的面积为（ ）| A、32cm2 |
| B、56cm2 |
| C、60cm2 |
| D、64cm2 |