题目内容
20．
如图，△ABC中，DE∥BC，若$\frac{AE}{EC}$=$\frac{1}{2}$，AD=5cm，BC=18cm，求DB和DE的长．
分析 由DE∥BC，判断△ADE∽△ABC，再由相似三角形的性质得出相似比求DE和DB的长即可．
解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∴AE：AC=DE：BC，
∵AE：EC=1：2，
∴AE：AC=A：3，
∴DE：BC=1：3，
∵BC=18cm，
∴DE=6cm，
∵AD：DB=AE：CE，AD=5cm，
∴5：DB=1：2，
∴DB=10cm．
点评 本题考查了相似三角形的判定与性质．关键是由平行线得出相似三角形，利用相似比求解．
练习册系列答案
阅读快车系列答案
相关题目
10．
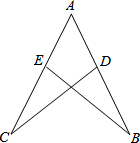如图，增加条件能判断△ACD≌△ABE的是（ ）
如图，增加条件能判断△ACD≌△ABE的是（ ）| A． | AC=AB，AD=AE | B． | ∠AEB=∠ADC | C． | AC=AB，CD=BE | D． | ∠C=∠B |
已知：如图，CD⊥AB，GF⊥AB，∠B=∠ADE，求证：∠1=∠2．
12．一个平面图形经过平移后，下列说法正确的是（ ）
①对应线段平行或在同一条直线上，
②对应线段相等，
③图形的大不形状都没有发生变化，
④对应点的连线段都平行．
①对应线段平行或在同一条直线上，
②对应线段相等，
③图形的大不形状都没有发生变化，
④对应点的连线段都平行．
| A． | ①②③ | B． | ②③④ | C． | ①②④ | D． | ①③④ |