题目内容
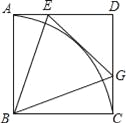
【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中![]() 为锐角,图2中
为锐角,图2中![]() 为直角,图3中
为直角,图3中![]() 为钝角).
为钝角).

在△ABC的边BC上取![]() ,
, ![]() 两点,使
两点,使![]() ,则
,则![]() ∽
∽![]() ∽
∽![]() ,
, ![]() ,
, ![]() ,进而可得
,进而可得![]()
![]() ;(用
;(用![]() 表示)
表示)
若AB=4,AC=3,BC=6,则![]()
![]() .
.
【答案】BC,BC, ![]() ,
, ![]() .
.
【解析】试题分析:
(1)由△ABC∽△B′BA∽△C′AC,可得![]() ,
, ![]() ,由此可得;AB2=B′B·BC,AC2=C′C·BC,由此可得AB2+AC2= B′B·BC+ C′C·BC=BC·(B′B+ C′C);
,由此可得;AB2=B′B·BC,AC2=C′C·BC,由此可得AB2+AC2= B′B·BC+ C′C·BC=BC·(B′B+ C′C);
(2)把AB=4,AC=3,BC=6,代入(1)中所得AB2+AC2= BC·(B′B+ C′C)可解得;B′B+ C′C=![]() ,结合B′B+ C′C=BC+B′C′即可解得:B′C′=
,结合B′B+ C′C=BC+B′C′即可解得:B′C′=![]() .
.
试题分析:
(1)∵△ABC∽△B′BA∽△C′AC,
∴![]() ,
, ![]() ,
,
∴ AB2=B′B·BC,AC2=C′C·BC,
∴AB2+AC2= B′B·BC+ C′C·BC=BC·(B′B+ C′C),即:AB2+AC2= BC·(B′B+ C′C);
故本题答案依次为:BC,BC,BC·(B′B+ C′C);
(2)由(1)可知AB2+AC2= BC·(B′B+ C′C),
∵AB=4,AC=3,BC=6,
∴16+9=6(B′B+ C′C),
∴B′B+ C′C=![]() ,
,
又∵B′B+ C′C=BC-B′C′,
∴B′C′=![]() .
.
即本题答案为: ![]() .
.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目