题目内容
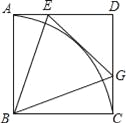
【题目】已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作![]() ,连结BG.
,连结BG.
(1)求证:EG与![]() 相切.
相切.
(2)求∠EBG的度数.
【答案】(1)证明见解析;(2)45°.
【解析】试题分析:(1)过点B作BF⊥EG,垂足为F,先证得△ABE≌△FBE,得出BF=BA,根据切线的判定即可证得结论;
(2)由△ABE≌△FBE得出∠FBE=∠ABE=![]() ∠ABF,然后根据切线长定理得出GF=GC,进而证得∠FBG=∠CBG=
∠ABF,然后根据切线长定理得出GF=GC,进而证得∠FBG=∠CBG=![]() ∠FBC,从而得出∠EBG=
∠FBC,从而得出∠EBG=![]() ∠ABC=45°.
∠ABC=45°.
试题解析:(1)过点B作BF⊥EG,垂足为F,
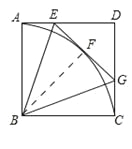
∴∠BFE=90°
∵四边形ABCD是正方形∴∠A=90°,∴∠BFE=∠A,
∵∠BEG=∠BEA,BE=BE, ∴△ABE≌△FBE, ∴BF=BA,
∵BA为![]() 的半径,∴BF为
的半径,∴BF为![]() 的半径,∴EG与
的半径,∴EG与![]() 相切;
相切;
(2)由(1)可得△ABE≌△FBE,∴∠1=∠ABE=![]() ∠ABF,
∠ABF,
∵四边形ABCD是正方形,∴∠C=∠ABC=90°,∴CD是⊙O切线,
由(1)可得EG与![]() 相切,∴GF=GC,
相切,∴GF=GC,
∵BF⊥EG,BC⊥CD,∴∠2=∠CBG=![]() ∠FBC,
∠FBC,
∴∠EBG=∠1+∠2=![]() (∠ABF+∠FBC)=
(∠ABF+∠FBC)= ![]() ∠ABC=45°
∠ABC=45°

练习册系列答案
相关题目