题目内容
【题目】化简(1)![]()
(2)![]()
(3)已知![]() 互为相反数,
互为相反数,![]() 是绝对值最小的有理数,求
是绝对值最小的有理数,求![]() 的值.
的值.
(4)先化简,再求值:![]() ,其中
,其中![]() 、
、![]() 满足
满足![]() .
.
【答案】(1)m![]() n+mn+4mn
n+mn+4mn![]() ;(2)13a12b;(3)1;(4)6
;(2)13a12b;(3)1;(4)6![]() .
.
【解析】
(1)先根据同类项的概念,找出此多项式中的同类项,再根据合并同类项的法则得出结果.注意不是同类项的不能合并.
(2)熟悉去括号法则:括号前面是负号,括号内的各项符号改变.合并同类项法则:只需把它们的系数相加减.
(3)利用非负数的性质确定x、y的值,再根据z是绝对值最小的有理数,确定z的值,即可解决问题.
(4)原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
(1)![]() =(5m
=(5m![]() n+6m
n+6m![]() n)+(2mn+3mn)+4mn
n)+(2mn+3mn)+4mn![]()
=m![]() n+mn+4mn
n+mn+4mn![]() .
.
(2)原式=4a6b6b+9a
=13a12b.
(3)∵![]() 互为相反数,
互为相反数,
∴(x+3) ![]() +|y2|=0,
+|y2|=0,
∴x=3,y=2,
∵z是绝对值最小的有理数,
∴z=0,
∴(x+y)![]() +xyz=(3+2)
+xyz=(3+2) ![]() +0=1,
+0=1,
故答案为1.
(4)原式=![]() x2x+
x2x+![]() y
y![]()
![]() x+
x+![]() y
y![]()
=3x+y![]() ,
,
∵(x+2) ![]() +|y
+|y![]() |=0,
|=0,
∴x=2,y=
则原式=6![]() .
.

 名师伴你成长课时同步学练测系列答案
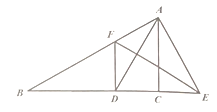
名师伴你成长课时同步学练测系列答案【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.

小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
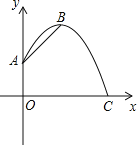
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.