题目内容
 如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,点G,H分别为AD,BC的中点,GH与BD交于点O,试证明EF和GH互相平分.
如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,点G,H分别为AD,BC的中点,GH与BD交于点O,试证明EF和GH互相平分.考点:平行四边形的判定与性质
专题:
分析:由平行四边形的性质,结合条件可证明△ABE≌△CDF,可得BE=DF,由条件可证明GO=HO,可证得结论.
解答:证明:∵四边形ABCD为平行四边形,
∴AB=CD,∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
又∵OB=OD,
∴OB-BE=OD-BF,即OE=OF,
又∵G,H分别为AD,BC的中点,
∴OG=OH=
AB=
CD,
∴EF和GH互相平分.
∴AB=CD,∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(AAS),
∴BE=DF,
又∵OB=OD,
∴OB-BE=OD-BF,即OE=OF,
又∵G,H分别为AD,BC的中点,
∴OG=OH=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF和GH互相平分.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
相关题目
二次函数y=-
x2+
x+1000的图象经过第一象限的整格点(即纵、横坐标是正整数的点) 共有( )个.
| 1 |
| 2 |
| 1999 |
| 2 |
| A、1 000 |
| B、1 001 |
| C、1 999 |
| D、2 001 |
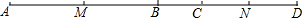 已知如图M是AB的中点,N是CD的中点,且MN=20,BC=8,求AD的长.
已知如图M是AB的中点,N是CD的中点,且MN=20,BC=8,求AD的长. 正比例函数y=kx和y=2kx(k是常数且k>0)的图象如图,它们与反比例函数y=
正比例函数y=kx和y=2kx(k是常数且k>0)的图象如图,它们与反比例函数y=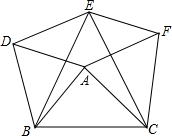 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF, 已知线段m,n,用尺规作一条线段AB,使AB=m+n.
已知线段m,n,用尺规作一条线段AB,使AB=m+n.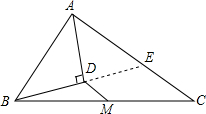 △ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.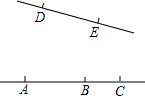 (1)如图,以点A、B、C、D、E中的任意3点为顶点的三角形共有
(1)如图,以点A、B、C、D、E中的任意3点为顶点的三角形共有 如图所示,△ABC中,AB=AC,∠C=30°,DA⊥AB于点A,若BC=6cm,求AB的长.
如图所示,△ABC中,AB=AC,∠C=30°,DA⊥AB于点A,若BC=6cm,求AB的长.