题目内容
20.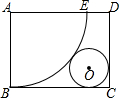 如图,将矩形纸片ABCD裁剪出扇形ABE和⊙O,其中⊙O与$\widehat{BE}$,BC,CD都相切.若扇形ABE与⊙O恰好制作成一个圆锥,已知AB=8cm,则AD的长为10.
如图,将矩形纸片ABCD裁剪出扇形ABE和⊙O,其中⊙O与$\widehat{BE}$,BC,CD都相切.若扇形ABE与⊙O恰好制作成一个圆锥,已知AB=8cm,则AD的长为10.
分析 首先求得弧AE的长,然后利用弧BE的长正好等于圆的底面周长,求得⊙O的半径,则BE的长加上半径即为AD的长.
解答 解:∵AB=8,∠A=90°,
∴$\widehat{BE}$=$\frac{90π•8}{180}$=4π,
∴⊙O的半径为2,
设⊙O与BC、CD分别相切于F、H,
连接FO并延长交AD于G,则FG垂直于AD,OH垂直于CD,连接OA.
可得矩形ABFG、矩形CDGF、矩形OHDG和正方形OFCH,
∴FE⊥BC,
∴OE=8-2=6,OA=8+2=10,
在Rt△AOG中,AG=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴AE=8=AG,
∴点E与G重合,
又DE=CF=2,
∴AD=AE+DE=10,
故答案为10.
点评 本题考查切线的性质、圆锥的计算、弧长公式、相切两圆的性质,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.

练习册系列答案
相关题目
10.下列说法中,正确的是( )
| A. | “打开电视,正在播放湖北新闻节目”是必然事件 | |
| B. | 某种彩票中奖概率为10%是指买十张一定有一张中奖 | |
| C. | “明天降雨的概率是50%表示明天有半天都在降雨” | |
| D. | “掷一次骰子,向上一面的数字是2”是随机事件 |
11. 如图,有下列命题:①若∠1=∠2,则∠D=∠3;②若∠C=∠D,则∠3=∠C;③若∠A=∠F,则∠1=∠2;④若∠1=∠2,∠C=∠D,则∠F=∠A,其中正确的个数为( )
如图,有下列命题:①若∠1=∠2,则∠D=∠3;②若∠C=∠D,则∠3=∠C;③若∠A=∠F,则∠1=∠2;④若∠1=∠2,∠C=∠D,则∠F=∠A,其中正确的个数为( )
 如图,有下列命题:①若∠1=∠2,则∠D=∠3;②若∠C=∠D,则∠3=∠C;③若∠A=∠F,则∠1=∠2;④若∠1=∠2,∠C=∠D,则∠F=∠A,其中正确的个数为( )
如图,有下列命题:①若∠1=∠2,则∠D=∠3;②若∠C=∠D,则∠3=∠C;③若∠A=∠F,则∠1=∠2;④若∠1=∠2,∠C=∠D,则∠F=∠A,其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.建科中学九(2)班5名同学在某一周零花钱分别为:30,25,25,40,35元,对于这组数据,以下说法中错误的是( )
| A. | 极差是15元 | B. | 平均数是31元 | C. | 众数是25元 | D. | 中位数是25元 |
5.某集团公司有9个子公司,各个子公司所创年利润的情况如下表所示.各子公司所创年利润的众数和中位数分别是( )
| 年利润(千万元) | 6 | 4 | 3 | 2 |
| 子公司个数 | 1 | 2 | 4 | 2 |
| A. | 4千万元,3千万元 | B. | 6千万元,4千万元 | C. | 6千万元,3千万元 | D. | 3千万元,3千万元 |

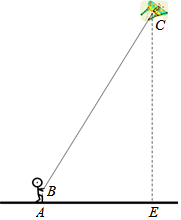 小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米,$\sqrt{3}$≈1.732)
小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米,$\sqrt{3}$≈1.732)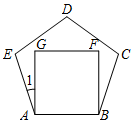 如图放置的一个正五边形ABCDE和正方形ABFG边长相等,则∠1=18度.
如图放置的一个正五边形ABCDE和正方形ABFG边长相等,则∠1=18度.