题目内容
17.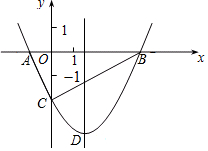 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A的坐标为(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A的坐标为(-1,0).(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,并证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△BCM的面积为5时,请直接写出M的坐标.
分析 (1)先把A点坐标为(-1,0)代入抛物线y=$\frac{1}{2}$x2+bx-2即可求出b的值,进而可求出抛物线的解析式,再由抛物线的顶点式即可求出其顶点坐标;
(2)由两点间的距离公式分别求出AC,BC,AB的长,再根据勾股定理即可判断出△ABC的形状;
(3)先求出直线BC解析式,求出平行于直线BC到直线BC距离为$\sqrt{5}$的直线a的解析式,联立方程组求解即可.
解答 解:(1)A点坐标为(-1,0)代入抛物线y=$\frac{1}{2}$x2+bx-2得,
0=$\frac{1}{2}$×(-1)2-b-2,解得b=-$\frac{3}{2}$,
∴原抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2,
∴x=$\frac{3}{2}$,y=-$\frac{25}{8}$,
∴D点坐标为:($\frac{3}{2}$,-$\frac{25}{8}$);
(2)∵抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2,令x=0,∴y=-2,∴C(0,-2);
令y=0,∴0=$\frac{1}{2}$x2-$\frac{3}{2}$x-2,∴x=-1或x=4,∴B(4,0)
∵AC=$\sqrt{5}$,BC=2$\sqrt{5}$,AB=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
(3)如图,过点O作OD⊥BC,
由(2)知,BC=2$\sqrt{5}$,OC=2,OB=4,∴OD=$\frac{4\sqrt{5}}{5}$,
设BC边上的高为h,
∴S△BCM=$\frac{1}{2}$×BC×h=$\frac{1}{2}$×2$\sqrt{5}$h=5,
∴h=$\sqrt{5}$,
∵$\frac{CE}{OC}=\frac{h}{OD}$,
∴$\frac{CE}{2}=\frac{\sqrt{5}}{\frac{4\sqrt{5}}{5}}$,
∴CE=$\frac{5}{2}$,
∵C(0,-2);B(4,0)
∴直线BC解析式为y=$\frac{1}{2}$x-2,
∴直线a的解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$②或y=$\frac{1}{2}$x-$\frac{9}{2}$③,
∵抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2①,
联立①②解得,$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$,
∴M(-1,0),(5,3);
联立①③得x2-4x+5=0,此方程无解,
∴M(-1,0),(5,3).
点评 此题是二次函数综合题,主要考查了抛物线与x轴的交点问题及勾股定理的逆定理,熟知坐标轴上各点坐标的特点及两点间的距离公式是解答此题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | x=2或x=-1 | B. | x=-1 | C. | x=±2 | D. | x=2 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
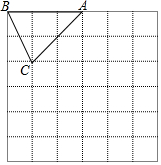 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.