题目内容
关于x的方程x2-(2m-1)x+m2-1=0的两实数根为x1,x2,且x12+x22=3,则m= .
考点:根与系数的关系,根的判别式
专题:计算题
分析:根据方程x2-(2m-1)x+m2-1=0的两实数根为x1,x2,得出x1+x2与x1x2的值,再根据x12+x22=3,即可求出m的值.
解答:解:∵方程x2-(2m-1)x+m2-1=0的两实数根为x1,x2,
∴x1+x2=2m-1,x1x2=m2-1,
∵x12+x22=(x1+x2)2-2x1x2=(2m-1)2-2(m2-1)=3,
解得:m1=0,m2=2,
∵方程有两实数根,
∴△=(2m-1)2-4(m2-1)≥0,
即m≤
∴m2=2(不合题意,舍去),
∴m=0;
故答案为:0.
∴x1+x2=2m-1,x1x2=m2-1,
∵x12+x22=(x1+x2)2-2x1x2=(2m-1)2-2(m2-1)=3,
解得:m1=0,m2=2,
∵方程有两实数根,
∴△=(2m-1)2-4(m2-1)≥0,
即m≤
| 5 |
| 4 |
∴m2=2(不合题意,舍去),
∴m=0;
故答案为:0.
点评:本题考查了根与系数的关系及根的判别式,难度适中,关键掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
一张试卷有25道题,做对一道题得4分,做错一道题扣1分,一个学生做完全部题目,总得分不低于70分,则他至少要答对( )道题.
| A、16 | B、17 | C、18 | D、19 |
 如图的图案是由一个菱形通过旋转得到的,每次旋转角度是( )
如图的图案是由一个菱形通过旋转得到的,每次旋转角度是( )| A、30° | B、45° |
| C、60° | D、90° |
 如图,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,则∠EOD=
如图,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,则∠EOD=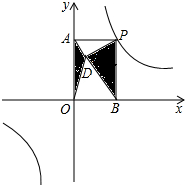 如图,点P是反比例函数y=
如图,点P是反比例函数y= 如图,菱形ABCD的边长为4,∠ABC=60°,则菱形的面积为
如图,菱形ABCD的边长为4,∠ABC=60°,则菱形的面积为