题目内容
10.某中学为了了解学生每天完成家庭作业所用时间的情况,从每班抽取相同数量的学生进行调查,并将所得数据进行整理,制成条形统计图和扇形统计图如图:(1)补全条形统计图;
(2)求扇形统计图扇形D的圆心角的度数;
(3)若该中学有2000名学生,请估计其中有多少名学生能在1.5小时内完成家庭作业?

分析 (1)根据A类的人数是10,所占的百分比是25%即可求得总人数,然后根据百分比的意义求得B类的人数;
(2)用360°乘以对应的比例即可求解;
(3)用总人数乘以对应的百分比即可求解.
解答 解:(1)抽取的总人数是:10÷25%=40(人),
在B类的人数是:40×30%=12(人).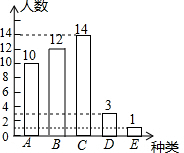 ;
;
(2)扇形统计图扇形D的圆心角的度数是:360×$\frac{3}{40}$=27°;
(3)能在1.5小时内完成家庭作业的人数是:2000×(25%+30%+35%)=1800(人).
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
5.一条公路,工程队第一天硬化路面$\frac{1}{6}$,第二天硬化剩余的$\frac{1}{5}$,下列说法正确的是( )
| A. | 第一天硬化的多 | B. | 第二天硬化的多 | C. | 两天硬化一样多 | D. | 无法确定 |
15.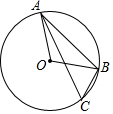 如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )
如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )
 如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )
如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )| A. | 40° | B. | 30° | C. | 45° | D. | 50° |
2.已知方程x2-6x+2=0,该方程用配方法变形后的结果为( )
| A. | (x-6)2=34 | B. | (x+6)2=34 | C. | (x-3)2=7 | D. | (x-3)2=11 |
19.若三角形中相等的两边长为5cm,第三边长为6cm,那么第三边上的高为( )
| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
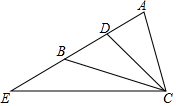 已知如图所示,在等腰△ABC中,AB=AC,CD是中线,延长AB到E,使得BE=AB,连结CE,求证:CD=$\frac{1}{2}$CE.
已知如图所示,在等腰△ABC中,AB=AC,CD是中线,延长AB到E,使得BE=AB,连结CE,求证:CD=$\frac{1}{2}$CE.