题目内容

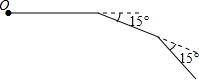如图，小明从点O出发，前进5m后向右转15°，再前进5m后又向右转15°，…这样一直下去，直到他第一次回到出发点O为止，他所走的路径构成了一个多边形．
（1）小明一共走了多少米？
（2）这个多边形的内角和是多少度？
考点：多边形内角与外角
专题：
分析：第一次回到出发点A时，所经过的路线正好构成一个外角是15度的正多边形，求得边数，即可求解．
解答：解：（1）∵所经过的路线正好构成一个外角是15度的正多边形，
∴360÷15=24，24×5=120m
答：小明一共走了120米；
（2）（24-2）×180°=3960°，
答：这个多边形的内角和是3960度．
点评：本题考查了正多边形的外角的计算以及多边形的内角和，第一次回到出发点A时，所经过的路线正好构成一个外角是15度的正多边形是关键．
练习册系列答案
相关题目
如图，已知四边形ABCD中，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形．
如图，已知△ABC和过点O的直线L．
（1）画出△ABC关于直线L对称的△A′B′C′；
（2）画出△ABC关于点O成中心对称的△A′′B′′C′′．
初中生的心理教育一直是教育工作者关注的问题之一，为此某学校对本校八年级学生进行了一次心理素质测试，测试总分为100分，分数取整数，为便于分层对学生进行心理辅导，学校按学生的测试成绩（x分）将学生分为三个层次，A级：x≥90；B级：60≤x＜90；C级：x＜60，并将测试结果绘制成统计图（不完整）．请根据图中提供的信息，回答下列问题：

（1）求此次参加心理素质测试的学生公有多少名？
（2）求此次心理素质测试为C级的学生占所有参加心理素质测试学生的百分比；
（3）此次心理素质测试成绩的中位数在
 
级层次中．
如图，已知四边形OABC、四边形OADE、四边形OFGH都是正方形．
（1）如图①，正方形OFGH的顶点F、H分别在边OA、OC上，连接AH、CF、EF，点M为CF的中点，连接OM，则线段AH与OM之间的数量关系是
 
，位置关系是
 

（2）如图②，将图①中的正方形OFGH绕点O顺时针旋转，旋转角为α（0＜α＜90°），其它条件不变，判断（1）中的两个结论是否仍然成立？若成立，请证明；若不成立，请说明理由．
（3）如图③，将将图①中的正方形OFGH绕点O顺时针旋转90°，使得点H落在边OA上，点F落在边OE上，点M为线段CF的中点，请你判断线段AH与OM之间的数量关系是否发生变化，写出你的猜想，并加以证明．
已知：等边△ABC的边长为3
3
，⊙O的半径为r．

（1）如图（1），若⊙O从与AC相切于点A的位置出发，在△ABC外部按顺时针方向沿三角形滚动，最后回到开始的位置．
①求圆心O经过的路径长（用含r的代数式表示）；
②当r=
3
2π
时，⊙O自转了几圈？
（2）如图（2），若将⊙O的圆心O与点A重合，然后将圆心O沿线路AC→CB→BA运动，最后回到点A，⊙O随点O的运动而移动．
①在移动过程中，⊙O与等边△ABC的边会有相切的位置关系，从切点的个数来考虑，相切有几种不同情况？写出不同情况下，r的取值范围及相应的切点个数．
②在移动过程中，在△ABC内部，⊙O未经过的部分的面积为S，在S＞0时，求S关于r的函数解析式，并写出自变量r的取值范围．
一份试卷共有25道选择题，每道选择题都给出了4个备选答案，其中只有一个是正确的，每道题选对得4分，不选或选错扣1分．小明同学解答这份试卷时得了90分，请你求出小明做对了几道题？
计算：
（1）（π-3.14）0-（
1
2
）-2+（
1
3
）2013×（-3）2013；
（2）（x-2）（x+3）-（x+3）2．
将x=
2
3
代入反比例函数y=-
1
x
中，所得函数值记为y1，又将x=y1+1代入原反比例函数中，所得函数值记为y2，再将x=y2+1代入原反比例函数中，所得函数值记为y3，…，如此继续下去，则y2014=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网