题目内容
6.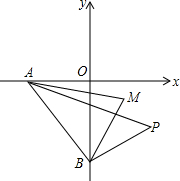 如图,已知P为第四象限一动点,A为x轴负半轴上一动点,B为y轴负半轴上一动点,若AM,BM分别平分∠OAP,∠OBP,试问A,B,P在运动过程中,∠P,∠M是否存在确定的数量关系?若存在,请证明你的结论;若不存在,请说明理由.
如图,已知P为第四象限一动点,A为x轴负半轴上一动点,B为y轴负半轴上一动点,若AM,BM分别平分∠OAP,∠OBP,试问A,B,P在运动过程中,∠P,∠M是否存在确定的数量关系?若存在,请证明你的结论;若不存在,请说明理由.
分析 如图,AP与y轴交于点C,与BM交于点D,根据角平分线的定义得到∠1=$\frac{1}{2}$∠OAC,∠2=$\frac{1}{2}$∠PBC,利用三角形内角和和对顶角相等,在△ADM和△BPM中得到∠1+∠M=∠2+∠P①,在△AOC和△BPC中得到∠OAC+∠AOC=∠PBC+∠P,即2∠1+90°=2∠2+∠P②,然后利用等式的性质变形易得2∠M-∠P=90°.
解答 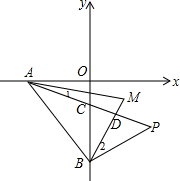 解:2∠M-∠P=90°.理由如下:
解:2∠M-∠P=90°.理由如下:
如图,AP与y轴交于点C,与BM交于点D,
∵AM,BM分别平分∠OAP,∠OBP,
∴∠1=$\frac{1}{2}$∠OAC,∠2=$\frac{1}{2}$∠PBC,
在△ADM和△BPM中,∠1+∠M=∠2+∠P①,
在△AOC和△BPC中,∠OAC+∠AOC=∠PBC+∠P,即2∠1+90°=2∠2+∠P②,
②-①×2得90°-2∠M=-∠P,
∴2∠M-∠P=90°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.利用三角形内角和可直接根据两已知角求第三个角或依据三角形中角的关系,用代数方法求三个角,也可在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图所示,点O在直线AB上,图中小于平角的角共有( )
如图所示,点O在直线AB上,图中小于平角的角共有( )
 如图所示,点O在直线AB上,图中小于平角的角共有( )
如图所示,点O在直线AB上,图中小于平角的角共有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
11.在Rt△ABC中,∠C=90°,如果三角形各边的长度都扩大2倍,则sinA的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 缩小2倍 | D. | 不能确定 |
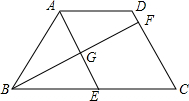 如图,在四边形ABCD中,∠BAD=∠ADC,∠ABC=∠BCD,∠BAD的角平分线AE与∠ABC的角平分线BF交于点G,
如图,在四边形ABCD中,∠BAD=∠ADC,∠ABC=∠BCD,∠BAD的角平分线AE与∠ABC的角平分线BF交于点G,
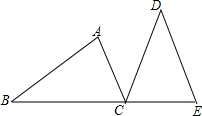 如图,C为BE上的一点,AC∥DE,AC=CE,∠ACD=∠B,△ABC与△CDE全等吗?请说明理由.
如图,C为BE上的一点,AC∥DE,AC=CE,∠ACD=∠B,△ABC与△CDE全等吗?请说明理由. 如图,点E,F,G,H分别在矩形ABCD的四条边AD,AB,BC,CD上,若∠AEF=20°,∠EFG=∠FGH=90°,则∠GHD=110°.
如图,点E,F,G,H分别在矩形ABCD的四条边AD,AB,BC,CD上,若∠AEF=20°,∠EFG=∠FGH=90°,则∠GHD=110°.