题目内容
17.游乐场有一个圆柱形的玩具吸引齐乐天,如图甲所示,从点A开始环绕圆柱有一架梯子,正好到达A点的正上方B点,已知圆柱的底面周长是12米,高AB为5米,则梯子最短是多少米呢?齐乐天想到圆柱的侧面展开图是长方形,如图乙所示,ABC是直角三角形,∠C=90,AC=12m,BC=5m.根据两点之间线段最短,所以线段AB的长就是梯子的最短长度.于是齐乐天利用勾股定理求出了AB的长,解决了问题,你也来试试吧.
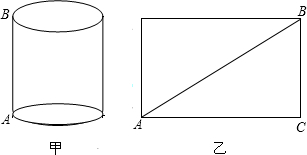
分析 根据题意画出圆柱的侧面展开图,利用勾股定理求解即可.
解答  解:如图所示,
解:如图所示,
∵∠C=90,AC=12m,BC=5m,
∴AB=$\sqrt{{AC}^{2}+{BC}^{2}}$=$\sqrt{{12}^{2}+{5}^{2}}$=13(cm).
答:梯子最短是13米.
点评 本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
8.若五边形ABCDE中,∠A=∠B=∠C,且∠D的外角为78°,∠D的外角与∠E互余,则∠B的度数是( )
| A. | 142° | B. | 140° | C. | 130° | D. | 150° |
7.已知四边形ABCD是平行四边形,则下列结论中正确的是( )
| A. | 当AB=BC时,?ABCD是正方形 | B. | 当AC⊥BD时,?ABCD是矩形 | ||
| C. | 当∠ABC=90°,?ABCD是矩形 | D. | 当AC=BD时,?ABCD是正方形 |
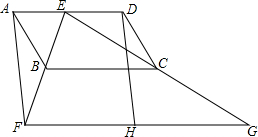 如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
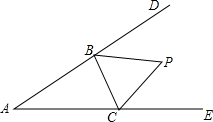 如图,在△ABC中,分别延长△ABC的边AB,AC到D,E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业时发现如下规律:
如图,在△ABC中,分别延长△ABC的边AB,AC到D,E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业时发现如下规律: 实数a,b在数轴上的位置如图所示,化简:$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{(a-b)^{2}}$.
实数a,b在数轴上的位置如图所示,化简:$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{(a-b)^{2}}$.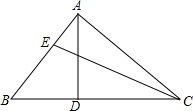 如图:在△ABC中,AD⊥BC于D,点E在BA上,∠ECB=30°,若EC=2$\sqrt{3}$且BE:AE=3:2,则AD=$\frac{5\sqrt{3}}{3}$.
如图:在△ABC中,AD⊥BC于D,点E在BA上,∠ECB=30°,若EC=2$\sqrt{3}$且BE:AE=3:2,则AD=$\frac{5\sqrt{3}}{3}$.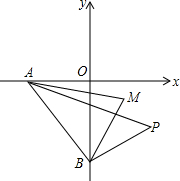 如图,已知P为第四象限一动点,A为x轴负半轴上一动点,B为y轴负半轴上一动点,若AM,BM分别平分∠OAP,∠OBP,试问A,B,P在运动过程中,∠P,∠M是否存在确定的数量关系?若存在,请证明你的结论;若不存在,请说明理由.
如图,已知P为第四象限一动点,A为x轴负半轴上一动点,B为y轴负半轴上一动点,若AM,BM分别平分∠OAP,∠OBP,试问A,B,P在运动过程中,∠P,∠M是否存在确定的数量关系?若存在,请证明你的结论;若不存在,请说明理由.