题目内容
6.观察下列等式:(1)1+2=$\frac{(1+2)×2}{2}$=3;
1+2+3=$\frac{(1+3)×3}{2}$=6;
6+7+8+9=$\frac{(6+9)×4}{2}$=30;
(2)10+11+12+13+14=60;
(3)猜想1+2+3+4+…+n=$\frac{n(n+1)}{2}$;
(4)利用猜想的规律结果计算67+68+69+…+200的值.
分析 (1)(2)(3)由题意可知:连续自然数的和等于两端的数相加乘数的个数除以2,由此规律逐一计算得出答案即可;
(4)利用得出的规律解答即可.
解答 解:(1)1+2=$\frac{(1+2)×2}{2}$=3;
1+2+3=$\frac{(1+3)×3}{2}$=6;
6+7+8+9=$\frac{(6+9)×4}{2}$=30;
(2)10+11+12+13+14=$\frac{(10+14)×5}{2}$=60;
(3)1+2+3+4+…+n=$\frac{n(n+1)}{2}$;
(4)67+68+69+…+200
=$\frac{134×(67+200)}{2}$
=17889.
故答案为:60,$\frac{n(n+1)}{2}$.
点评 此题考查数字的变化规律,找出数字排列的规律,得出运算的一般方法解决问题.

练习册系列答案
相关题目
17.2015年宁波市前8个月新增贷款72000000000,用科学记数法表示为( )
| A. | 7.2×108 | B. | 7.2×109 | C. | 7.2×1010 | D. | 7.2×1011 |
18.某村组织20辆汽车装运A、B、C三种水果共100吨到外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种水果且必须装满,且装运A、B水果的车辆数都不少于4辆.设装运A水果的车辆为x,装运B水果的车辆数为y,运费最低为2240元.
| 水果种类 | A | B | C |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨所需运费(元/吨) | 120 | 160 | 100 |

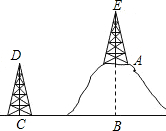 如图,小山高AB=75米,B,C两点间的水平距离为40米,两铁塔的高相等,即CD=AE.如果要在两铁塔顶D,E间架设一条高压线,那么这条高压线至少为多长?
如图,小山高AB=75米,B,C两点间的水平距离为40米,两铁塔的高相等,即CD=AE.如果要在两铁塔顶D,E间架设一条高压线,那么这条高压线至少为多长?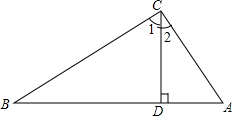 已知:如图,△ABC中,∠BCA=90°,CD⊥AB于点D.
已知:如图,△ABC中,∠BCA=90°,CD⊥AB于点D.