题目内容
1.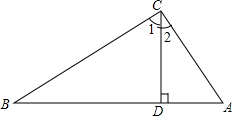 已知:如图,△ABC中,∠BCA=90°,CD⊥AB于点D.
已知:如图,△ABC中,∠BCA=90°,CD⊥AB于点D.(1)求证:BC2=BD•BA;
(2)若AD=$\frac{9}{5}$,BC=4,求AC、BD.
分析 (1)由已知条件得到∠BCA=∠BDC=90°,由∠B=∠B,推出△BCD∽△ABC,根据相似三角形的性质即可得到结论.
(2)由(1)证得BC2=BD•BA,把AD=$\frac{9}{5}$,BC=4代入上式即可得到BD=$\frac{16}{5}$,通过△ACD∽△ABC,得到$\frac{AC}{AB}=\frac{AD}{AC}$,根据相似三角形即可得到结论.
解答 (1)证明:∵ ∠BCA=90°,CD⊥AB于点D,
∠BCA=90°,CD⊥AB于点D,
∴∠BCA=∠BDC=90°,
∵∠B=∠B,
∴△BCD∽△ABC,
∴$\frac{BC}{AB}=\frac{BD}{BC}$,
∴BC2=BD•BA;
(2)解:由(1)证得BC2=BD•BA,
∵AD=$\frac{9}{5}$,BC=4,
∴42=BD(BD+$\frac{9}{5}$),
解得:BD=$\frac{16}{5}$,
∵∠BCA=∠ADC=90°,
∵∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∴AC2=AB•AD=5×$\frac{9}{5}$=9,
∴AC=3.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
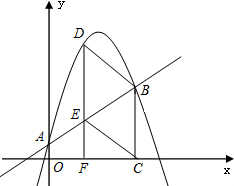 如图,抛物线y=-$\frac{5}{4}$x2+bx+c与直线y=$\frac{1}{2}$x+c相交于A(0,1),B(3,$\frac{5}{2}$)两点,过点B作BC⊥x轴,垂足为点C,在线段AB上方的抛物线上取一点D,过D作DF⊥x轴,垂足为点F,交AB于点E.
如图,抛物线y=-$\frac{5}{4}$x2+bx+c与直线y=$\frac{1}{2}$x+c相交于A(0,1),B(3,$\frac{5}{2}$)两点,过点B作BC⊥x轴,垂足为点C,在线段AB上方的抛物线上取一点D,过D作DF⊥x轴,垂足为点F,交AB于点E.