题目内容
2.已知函数y=x2-mx+m-2.(1)求证:无论m取什么值,它的图象与x轴总有两个交点;
(2)当m取何值时,这两个交点间的距离最小?并求出最小距离.
分析 (1)令二次函数解析式中y=0,得到关于x的一元二次方程,解方程即可;
(2)由(1)知图象与x轴的两个交点,用m表示出|x1-x2|,再求出最小值即可.
解答 解:(1)令y=0,得:x2-mx+m-2=0,
则△=m2-4(m-2)=m2-4m+8=(m-2)2+4,
∵(m-2)2≥0,
∴(m-2)2+4>0,
无论m取什么值,它的图象与x轴总有两个交点;
(2)设二次函数图象与x轴交点的横坐标为x1,x2;
根据(1)可知,x1+x2=m,x1x2=m-2,
∴|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(m-2)^{2}+4}$,
要使抛物线的图象与x轴的两个交点的距离最小,即|当m=2时,|x1-x2|最小,此时最小值为2.
点评 本题考查了抛物线与x轴的交点,二次函数与一元二次方程的关系,求出抛物线与x轴的两交点坐标是解决问题的关键.

练习册系列答案
相关题目
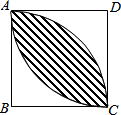 如图所示,若正方形边长为a,则阴影部分的面积为($\frac{1}{2}$π-1)a2.
如图所示,若正方形边长为a,则阴影部分的面积为($\frac{1}{2}$π-1)a2.