题目内容
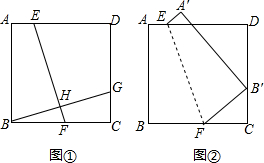 探究:如图①,在正方形ABCD中,E、F、G分别是边AD、BC、CD上的点,BG⊥EF,垂足为H.求证:EF=BG.
探究:如图①,在正方形ABCD中,E、F、G分别是边AD、BC、CD上的点,BG⊥EF,垂足为H.求证:EF=BG.应用:如图②,将正方形ABCD翻折,使点B落在边CD上的点B′处,折痕为EF.若AE=2,BF=6,则B′C=
考点:正方形的性质,全等三角形的判定与性质,翻折变换(折叠问题)
专题:
分析:探究:过点E作EM⊥BC于M,可得四边形ABME是矩形,根据矩形的对边相等可得AB=EM,再根据正方形的四条边都相等可得AB=BC,从而得到EM=BC,再根据等角的余角相等求出∠CBG=∠MEF,然后利用“角边角”证明△BCG和△EMF全等,根据全等三角形对应边相等即可得证;
应用:连接BB′过点E作EM⊥BC于M,根据折叠的性质可得EF⊥BB′,先求出MF,再根据探究结论B′C=MF.
应用:连接BB′过点E作EM⊥BC于M,根据折叠的性质可得EF⊥BB′,先求出MF,再根据探究结论B′C=MF.
解答:探究:证明:如图,过点E作EM⊥BC于M,则四边形ABME是矩形,
∴AB=EM,
在正方形ABCD中,AB=BC,
∴EM=BC,
∵EM⊥BC,
∴∠MEF+∠EFM=90°,
∵BG⊥EF,
∴∠CBG+∠EMF=90°,
∴∠CBG=∠MEF,
在△BCG和△EMF中,
,
∴△BCG≌△EMF(ASA),
∴EF=BG;
应用:解:如图,连接BB′过点E作EM⊥BC于M,
∵点B沿EF折叠后落在边CD上的点B′处,
∴EF⊥BB′,
∵AE=2,BF=6,
∴MF=BF-BM=BF-AE=6-2=4,
根据探究,△BCG≌△EMF,
∴B′C=MF=4.
故答案为:4.
∴AB=EM,
在正方形ABCD中,AB=BC,
∴EM=BC,
∵EM⊥BC,
∴∠MEF+∠EFM=90°,
∵BG⊥EF,

∴∠CBG+∠EMF=90°,
∴∠CBG=∠MEF,
在△BCG和△EMF中,
|
∴△BCG≌△EMF(ASA),
∴EF=BG;
应用:解:如图,连接BB′过点E作EM⊥BC于M,
∵点B沿EF折叠后落在边CD上的点B′处,
∴EF⊥BB′,
∵AE=2,BF=6,
∴MF=BF-BM=BF-AE=6-2=4,
根据探究,△BCG≌△EMF,
∴B′C=MF=4.
故答案为:4.
点评:本题考查了正方形的性质,全等三角形的应用,折叠的性质,等角的余角相等的性质,作辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
代数式
,-
x,
中是分式的有( )
| 1 |
| x |
| 3 |
| 2 |
| 4 |
| x-7 |
| A、1个 | B、2个 | C、3个 | D、0个 |
不等式组
的解集,在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
已知反比例函数y=
的图象过点(-2,-4),则k的值是( )
| k-2 |
| x |
| A、10 | B、-6 | C、8 | D、-8 |
 如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=EB,若∠D=40°,则∠BEC的度数为
如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=EB,若∠D=40°,则∠BEC的度数为 如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点上
如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点上