题目内容
如图，已知⊙O的弦CD垂直于直径AB，点E在CD上，且EC=EB，若∠D=40°，则∠BEC的度数为考点：垂径定理
专题：
分析：先根据垂径定理得出
=
，故可得出BD=BC，由此可得出∠C的度数，再根据EC=EB可得出∠C=∠EBC，由三角形内角和定理即可得出结论．
 |
| BD |
|
| BC |
解答：解：∵⊙O的弦CD垂直于直径AB，∠D=40°，
∴
=
，
∴BD=BC，
∴∠C=∠D=40°，
∵EC=EB，
∴∠C=∠EBC=40°，
∴∠BEC=180°-∠C-∠EBC=180°-40°-40°=100°．
故答案为：100°．
∴
|
| BD |
|
| BC |
∴BD=BC，
∴∠C=∠D=40°，
∵EC=EB，
∴∠C=∠EBC=40°，
∴∠BEC=180°-∠C-∠EBC=180°-40°-40°=100°．
故答案为：100°．
点评：本题考查的是垂径定理，即垂直于弦的直径平分弦，并且平分弦所对的弧．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
已知甲、乙、丙三个旅行团的游客人数都相等，且毎一个旅行团游客的平均年龄都是35岁，这三个旅行团游客年龄的方差分别是S甲2=17，S乙2=14.6，S丙3=19，如果你最喜欢带游客年龄相近的旅行团，若在三个旅行团中选一个，则你应选择（ ）
| A、甲团 | B、乙团 |
| C、丙团 | D、采取抽签方式，随便选一个 |
对于任意a，都有点A（a+1，2a+3）在直线l上，则直线l不经过的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在格点上，在建立平面直角坐标系后，点A的坐标为（-7，1），点B的坐标为（-3，1），点C的坐标为（-3，3）．
如图水库大坝横断面为梯形ABCD，坝顶7米，坝高CE，DE=8米，CD=10米，下底AD=27米，背水坡AB的坡度为（ ）| A、1：3 | B、1：2 |
| C、1：2.5 | D、1：1.5 |
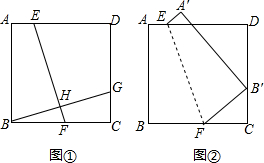探究：如图①，在正方形ABCD中，E、F、G分别是边AD、BC、CD上的点，BG⊥EF，垂足为H．求证：EF=BG．