题目内容
 如图,在△ABC中,∠ACB=90°,CD为边AB上的高,已知BD=1,则线段AD的长是( )
如图,在△ABC中,∠ACB=90°,CD为边AB上的高,已知BD=1,则线段AD的长是( )| A、sin2A |
| B、cos2A |
| C、tan2A |
| D、cot2A |
考点:相似三角形的判定与性质,锐角三角函数的定义
专题:
分析:由在△ABC中,∠ACB=90°,CD为边AB上的高,易证得△ACD∽△CBD,根据相似三角形的对应边成比例,且BD=1,可得AD=CD2,又由cot∠A=cot∠BCD=
=CD,即可求得答案.
| CD |
| BD |
解答:解:∵在△ABC中,∠ACB=90°,CD为边AB上的高,
∴∠ADC=∠CDB=90°,∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠ACD=∠BCD,
∴△ACD∽△CBD,
∴
=
,
∵BD=1,
∴AD=CD2,
∵cot∠A=cot∠BCD=
=CD,
∴CD=cotA,
∴AD=cot2A.
故选D.
∴∠ADC=∠CDB=90°,∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠ACD=∠BCD,
∴△ACD∽△CBD,
∴
| AD |
| CD |
| CD |
| BD |
∵BD=1,
∴AD=CD2,
∵cot∠A=cot∠BCD=
| CD |
| BD |
∴CD=cotA,
∴AD=cot2A.
故选D.
点评:此题考查了相似三角形的判定与性质以及三角函数等知识.此题难度适中,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
在
、1.732、
,、-
四个数中,其中是无理数的是( )
| ||
| 2 |
| 16 |
| 22 |
| 7 |
A、
| ||||
| B、1.732 | ||||
C、
| ||||
D、-
|
若(k-1)x|k|+20=0是一元一次方程,则k的值是( )
| A、1 | B、-1 | C、0 | D、±1 |
| ||
| y2+y+1 |
| (y-2)2 |
| x2+x+1 |
| A、-1 | B、0 | C、2 | D、1 |
如果关于x的方程x2+kx+
k2-3k+
=0的两个实数根分别为x1,x2,那么
的值为( )
| 3 |
| 4 |
| 9 |
| 2 |
| ||
|
A、-
| ||
B、
| ||
C、
| ||
D、-
|

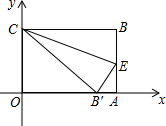 如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tanOB′C=
如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tanOB′C=