题目内容
10.在半径为4的⊙O中,点C是以AB为直径的半圆弧的中点,OD⊥AC,垂足为D点,点E是射线AB上的任意一点,DF∥AB,DF与CE交于点F,设EF=x,DF=y.(1)如图1,当点E在射线OB上时,求y与x的函数关系式,并写出自变量x的取值范围;
(2)如图2,当点F在⊙O上时,求线段DF的长;
(3)如果以点E为圆心、EF为半径的圆与⊙O相切,请直接写出线段DF的长.
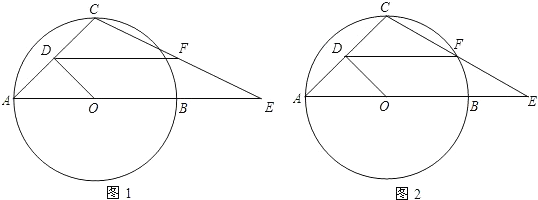
分析 (1)连接OC,如图1,根据垂径定理可得OD=AD,根据平行线分线段成比例可得CF=EF,根据三角形的中位线定理可得DF=$\frac{1}{2}$AE.由点C是以AB为直径的半圆的中点可得∠AOC=∠BOC=90°,根据勾股定理可用x的代数式表示OE,从而表示出AE,DF,即可解决问题;
(2)当点F在⊙O上时,连接OC、OF,如图2,根据直角三角形斜边上的中线等于斜边的一半可得OF=EF=CF=4,即x=4,代入(1)中y与x的函数关系式,即可解决问题;
(3)由于两圆相切包括外切与内切,因此需分情况讨论,可分三种情况(①⊙E与⊙O外切于点B,②⊙E与⊙O内切于点B,③⊙E与⊙O内切于点A)讨论,用x的代数式表示出OE,代入CE2-OE2=CO2,求出x,就可解决问题.
解答 解:(1)连接OC,如图1.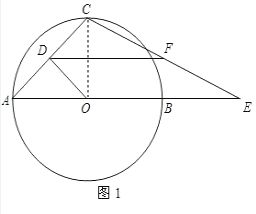
∵AC是⊙O的弦,OD⊥AC,
∴OD=AD.
∵DF∥AB,
∴CF=EF,
∴DF=$\frac{1}{2}$AE=$\frac{1}{2}$(AO+OE).
∵点C是以AB为直径的半圆的中点,
∴∠AOC=∠BOC=90°.
∵EF=x,AO=CO=4,
∴CE=2x,OE=$\sqrt{C{E}^{2}-O{C}^{2}}$=$\sqrt{4{x}^{2}-{4}^{2}}$=2$\sqrt{{x}^{2}-4}$,
∴y=$\frac{1}{2}$(4+2$\sqrt{{x}^{2}-4}$)=2+$\sqrt{{x}^{2}-4}$,自变量x的取值范围为x≥2;
(2)当点F在⊙O上时,连接OC、OF,如图2,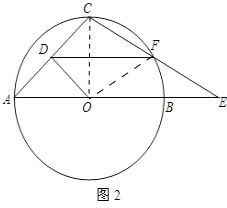
则有OF=EF=CF=4,即x=4,
∴DF=2+$\sqrt{{4}^{2}-4}$=2+2$\sqrt{3}$;
(3)①当⊙E与⊙O外切于点B时,
则有BE=FE=x,OE=x+4.
∵CE2-OE2=CO2,
∴(2x)2-(x+4)2=42,
整理得:3x2-8x-32=0,
∴x1=$\frac{4+4\sqrt{7}}{3}$,x2=$\frac{4-4\sqrt{7}}{3}$(舍去),
∴DF=$\frac{1}{2}$(AB+BE)=$\frac{1}{2}$(8+$\frac{4+4\sqrt{7}}{3}$)=$\frac{14+2\sqrt{7}}{3}$.
②当⊙E与⊙O内切于点B时,
则有BE=FE=x,OE=4-x.
∵CE2-OE2=CO2,
∴(2x)2-(4-x)2=42,
整理得:3x2+8x-32=0,
∴x1=$\frac{-4+4\sqrt{7}}{3}$,x2=$\frac{-4-4\sqrt{7}}{3}$(舍去).
∴DF=$\frac{1}{2}$(AB-BE)=$\frac{1}{2}$(8-$\frac{-4+4\sqrt{7}}{3}$)=$\frac{14-2\sqrt{7}}{3}$.
③当⊙E与⊙O内切于点A时,
则有AE=FE=x,OE=4-x.
∵CE2-OE2=CO2,
∴(2x)2-(4-x)2=42,
整理得:3x2+8x-32=0,
∴x1=$\frac{-4+4\sqrt{7}}{3}$,x2=$\frac{-4-4\sqrt{7}}{3}$(舍去),
∴DF=$\frac{1}{2}$AE=$\frac{2\sqrt{7}-2}{3}$.
点评 本题主要考查了垂径定理、平行线分线段成比例、三角形的中位线定理、弧与圆心角的关系、勾股定理、相切两圆的数量关系、解一元二次方程、直角三角形斜边上的中线等于斜边的一半等知识,还用到了分类讨论的数学思想,利用CE2-OE2=CO2是解决本题的关键.

| A. | 1+$\sqrt{23}$ | B. | 4+$\sqrt{26}$ | C. | 4+$\sqrt{15}$ | D. | 4+$\sqrt{3}$ |
 如图,点Q在直线y=-x上运动,点A的坐标为(3,0),点B的坐标为(0,2),当AQ+BQ最短时,点Q的坐标为(0,0).
如图,点Q在直线y=-x上运动,点A的坐标为(3,0),点B的坐标为(0,2),当AQ+BQ最短时,点Q的坐标为(0,0).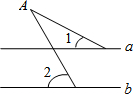 如图,已知直线a∥b,∠1=28°,∠2=52°,那么∠A的度数是24°.
如图,已知直线a∥b,∠1=28°,∠2=52°,那么∠A的度数是24°.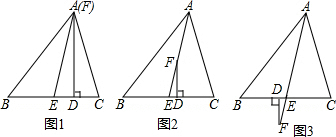
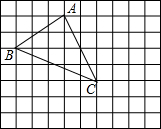 如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1),
如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1),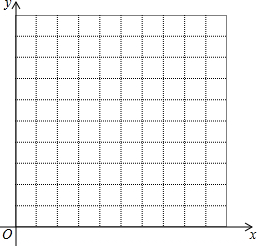 在平面直角坐标系中,点P从原点O出发,且点P只能每次向上平移2个单位长度或向右平移1个单位长度.
在平面直角坐标系中,点P从原点O出发,且点P只能每次向上平移2个单位长度或向右平移1个单位长度.