题目内容
6. 如图,平行四边形ABCD中,E是边BC的中点,AE交BD于点F,如果BF=4,那么FD=8.
如图,平行四边形ABCD中,E是边BC的中点,AE交BD于点F,如果BF=4,那么FD=8.
分析 由平行四边形ABCD得AD=BC,AD∥BC,于是得到△ADF∽△EBF,根据相似三角形的性质便得到结论.
解答 解:∵平行四边形ABCD,E是边BC的中点,
∴AD=BC,
∴AD∥BC,
∴$\frac{BE}{AD}=\frac{1}{2}$,
∴△ADF∽△EBF,
∴$\frac{BF}{DF}=\frac{BE}{AD}=\frac{1}{2}$,
∵BF=4,
∴DF=8,
故答案为8.
点评 本题主要考查了平行四边形和相似三角形的判定和性质,灵活应用这些性质是解决问题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
14.抛物线y=-5x2+x+7与坐标轴的交点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |

 已知函数y=ax2+bx+c的图象如图所示:则△>0;a>0;b<0;c<0;a+b+c<0;a-b+c>0.
已知函数y=ax2+bx+c的图象如图所示:则△>0;a>0;b<0;c<0;a+b+c<0;a-b+c>0. 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上,若AD=4,BE=1,求:
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上,若AD=4,BE=1,求: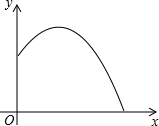 如图是某运动员打羽毛球的抛物线示意图,已知打出羽毛球的高度y(m)与水平距离x(m)之间的函数关系式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+7,则该羽毛球落地时距离发出点( )
如图是某运动员打羽毛球的抛物线示意图,已知打出羽毛球的高度y(m)与水平距离x(m)之间的函数关系式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+7,则该羽毛球落地时距离发出点( )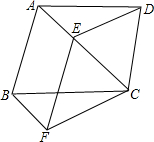 如图,四边形ABCD的AB边平行于CD边,在对角线上取一点E,使∠DEC=∠ABC,若CE:CD=CD:CA.
如图,四边形ABCD的AB边平行于CD边,在对角线上取一点E,使∠DEC=∠ABC,若CE:CD=CD:CA.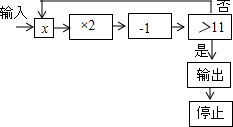 如图为某一运算程序,规定:程序运行到判断“结果是否大于11”为一次运算,若输入整数x后,运算进行了2次就输出停止,则满足条件的整数x是4、5或6.
如图为某一运算程序,规定:程序运行到判断“结果是否大于11”为一次运算,若输入整数x后,运算进行了2次就输出停止,则满足条件的整数x是4、5或6.