题目内容
如图,在直线L上依次取三点A、B、C,BC>AB且BC=a,在直线L的同侧作两个黄金矩形ABDE和BCGF,即AE:AB=FB:BC=(
-1):2,连接EF,EC,FC,则△CEF的面积等于 .

| 5 |

考点:黄金分割
专题:计算题
分析:设AB=b,根据黄金矩形的定义得到AE=
b,FB=
a,然后根据S△CEF=S梯形ABFE+S矩形BCGF-
S△ACE-
S△CFG进行计算.
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设AB=b,
∵AE:AB=FB:BC=(
-1):2,
∴AE=
b,FB=
a,
∴S△CEF=S梯形ABFE+S矩形BCGF-
S△ACE-
S△CFG
=
•(
b+
a)•b+
a2-
b(a+b)-
•
a2
=
(b2+ab+2a2-ab-b2-a2)
=
a2.
故答案为
a2.
∵AE:AB=FB:BC=(
| 5 |
∴AE=
| ||
| 2 |
| ||
| 2 |
∴S△CEF=S梯形ABFE+S矩形BCGF-
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 4 |
=
| ||
| 4 |
故答案为
| ||
| 4 |
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,在△ABC中,∠B=40°,三角形的外角△DAC和∠ACF的平分线交于点E,则∠AEC=
如图,在△ABC中,∠B=40°,三角形的外角△DAC和∠ACF的平分线交于点E,则∠AEC= 如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为
如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为
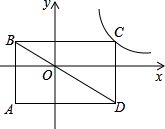 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数y=