题目内容
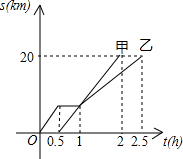甲、乙两同学骑自行车从A地沿同一条路到B地，已知乙比甲先出发，他们离出发地的距离s（km）与骑行时t（h）之间的函数关系如图所示，给出下列说法：①他们都骑行了20km；②相遇后，甲的速度小于乙的速度；③甲、乙两人同时到达目的地；
根据图象信息以上结论正确的有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
考点：一次函数的应用
专题：
分析：①由函数图象可以直接得出甲、乙两同学行驶的路程是20km；
②由函数图象可以直接求出甲的速度，就可以求出乙的速度，比较大小即可；
③由函数知己额可以得出甲比乙先到达目的地；
②由函数图象可以直接求出甲的速度，就可以求出乙的速度，比较大小即可；
③由函数知己额可以得出甲比乙先到达目的地；
解答：解：①由函数图象得甲、乙两同学行驶的路程是20km，故正确
②由函数图象，得
甲的速度为：20÷1.5=
km/h，
甲、乙相遇后，乙的速度为：（20-
×
）÷1.5=
．
∵
＞
，
∴相遇后，甲的速度大于乙的速度，故错误．
③由函数图象得出，甲比乙先到达目的地．故错误，
综上所述，正确的结论只有1个．
故选D．
②由函数图象，得
甲的速度为：20÷1.5=
| 40 |
| 3 |
甲、乙相遇后，乙的速度为：（20-
| 40 |
| 3 |
| 1 |
| 2 |
| 80 |
| 9 |
∵
| 40 |
| 3 |
| 80 |
| 9 |
∴相遇后，甲的速度大于乙的速度，故错误．
③由函数图象得出，甲比乙先到达目的地．故错误，
综上所述，正确的结论只有1个．
故选D．
点评：本题考查了一次函数的图象的性质的运用，行程问题的数量关系速度=路程后÷时间的运用，有理数大小的比较的运用，解答时理解函数的图象的含义是关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，过点C（0，4）的直线l1与过点O的直线l2交于点B（2若a，b是有理数，且
=0，则（ ）
| a |
| b |
| A、a=0且b≠0 |
| B、a=0 |
| C、a=0或b=0 |
| D、a，b同号 |
