Question

13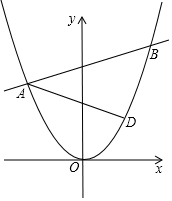．如图，点D（2，2）在抛物线y=$\frac{1}{2}$x²上，直线AB：y=kx+b交抛物线于A、B两点（A、B不与点D重合）．若∠ADB=90°．求证：直线AB过定点，并求出该定点的坐标．

Answer 1

分析 设A（m，$\frac{1}{2}$m²），B（n，$\frac{1}{2}$n²），m≠n≠2，则直线AD的斜率K_AD=$\frac{2-\frac{1}{2}{m}^{2}}{2-m}$=$\frac{1}{2}$（2+m），直线BD的斜率K_BD=$\frac{1}{2}$（2+n），由K_AD•K_BD=-1，可得mn+2（m+n）+8=0，因为A、B在直线AB上，所以$\left\{\begin{array}{l}{\frac{1}{2}{m}^{2}=mk+b}\\{\frac{1}{2}{n}^{2}=nk+b}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=\frac{1}{2}（m+n）}\\{b=-\frac{1}{2}mn}\end{array}\right.$，直线AB的解析式为y=$\frac{1}{2}$（m+n）x-$\frac{1}{2}$mn，将mn=-8-2（m+n）代可得y=$\frac{1}{2}$（m+n）x-$\frac{1}{2}$[-8-2（m+n）]=$\frac{1}{2}$（m+n）x+4+m+n=$\frac{1}{2}$（m+n）（x+2）+4，故经过定点（-2，4）．

解答 解：设A（m，$\frac{1}{2}$m²），B（n，$\frac{1}{2}$n²），m≠n≠2，则直线AD的斜率K_AD=$\frac{2-\frac{1}{2}{m}^{2}}{2-m}$=$\frac{1}{2}$（2+m），直线BD的斜率K_BD=$\frac{1}{2}$（2+n），
∵∠ADB=90°，
∴K_AD•K_BD=-1，
∴$\frac{1}{2}$（2+m）•$\frac{1}{2}$（2+n）=-1，
可得mn+2（m+n）+8=0，
∵A、B在直线AB上，$\left\{\begin{array}{l}{\frac{1}{2}{m}^{2}=mk+b}\\{\frac{1}{2}{n}^{2}=nk+b}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=\frac{1}{2}（m+n）}\\{b=-\frac{1}{2}mn}\end{array}\right.$，
∴直线AB的解析式为y=$\frac{1}{2}$（m+n）x-$\frac{1}{2}$mn，
将mn=-8-2（m+n）代可得y=$\frac{1}{2}$（m+n）x-$\frac{1}{2}$[-8-2（m+n）]=$\frac{1}{2}$（m+n）x+4+m+n=$\frac{1}{2}$（m+n）（x+2）+4，
∴x=-2时，y=4，
∴直线AB经过定点（-2，4）．

点评 本题考查二次函数图象上点的特征、一次函数的应用，解题的关键是学会利用参数解决问题，题目比较难，属于竞赛题．