题目内容
17.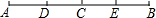 如图,已知C是AB的中点,D是AC的中点,E是BC的中点.
如图,已知C是AB的中点,D是AC的中点,E是BC的中点.(1)若AB=10cm,求DE的长度.
(2)若CE=3cm,求DB的长度.
分析 (1)根据中点的性质求得CD=$\frac{1}{2}$AC,CE=$\frac{1}{2}$BC,根据等量关系即可得到DE的长度.
(2)根据中点的性质求得BC,再根据中点的性质求得AC的长,再根据中点的性质求得CD,再根据等量关系可得到DB的长度.
解答 解:(1)∵D是AC的中点,E是BC的中点,
∴CD=$\frac{1}{2}$AC,CE=$\frac{1}{2}$BC,
∴DE=CD+CE=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB=5cm;
(2)∵E是BC的中点,
∴BC=2CE=6cm,
∵C是AB的中点,
∴AC=BC=cm,
∵D是AC的中点,
∴CD=3cm,
∴DB=DC+CB=9cm.
点评 本题考查的是两点间的距离的计算,掌握线段中点的性质是解题的关键.

练习册系列答案
相关题目
 有理数a、b、c在数轴上的位置如图所示,那么|a-b|-|1-b|+|c-1|=2-a-c.
有理数a、b、c在数轴上的位置如图所示,那么|a-b|-|1-b|+|c-1|=2-a-c. 如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数.
如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数. 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.