题目内容
9.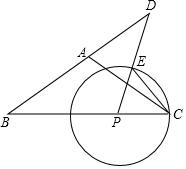 如图,在△ABC中,AB=AC=5,cosB=$\frac{4}{5}$,点P为边BC上一动点,过点P作射线PE交射线BA于点D,∠BPD=∠BAC,以点P为圆心,PC长为半径作⊙P交射线PD于点E,联结CE,设BD=x,CE=y.
如图,在△ABC中,AB=AC=5,cosB=$\frac{4}{5}$,点P为边BC上一动点,过点P作射线PE交射线BA于点D,∠BPD=∠BAC,以点P为圆心,PC长为半径作⊙P交射线PD于点E,联结CE,设BD=x,CE=y.(1)当⊙P与AB相切时,求⊙P的半径;
(2)当点D在BA的延长线上时,求y关于x的函数解析式,并写出它的定义域;
(3)如果⊙O与⊙P相交于点C、E,且⊙O经过点B,当OP=$\frac{5}{4}$时,求AD的长.
分析 (1)作PF⊥BD于F,作AH⊥BC于H,如图,设⊙P的半径为r,根据等腰三角形的性质得BH=CH,再通过解直角三角形得到BH=4,AH=3,则BC=2BH=8,sinB=$\frac{3}{5}$,接着在Rt△BPH中利用正弦的定义得到PF=$\frac{3}{5}$(8-r),然后根据切线的性质得$\frac{3}{5}$(8-r)=r,再解方程求出r即可;
(2)先证明△BDP∽△BCA,利用相似比得到r=8-$\frac{5}{8}$x,作PG⊥CE于G,如图,利用垂径定理得到CG=EG=$\frac{1}{2}$y,再证明FP⊥PG,所以∠GPC=∠B,接着在Rt△PGC中利用正弦定义得到$\frac{1}{2}$y=$\frac{3}{5}$r,则$\frac{1}{2}$y=$\frac{3}{5}$(8-$\frac{5}{8}$x),然后用x表示y,同时写出x的取值范围;
(3)根据三角形外心性质可判定点O为AH和GP的交点,如图,在Rt△OPH中,利用三角函数可计算出PH=1,讨论:当点D在AB上,此时r=5,则8-$\frac{5}{8}$x=5,解方程求出x后计算5-x即可得到AD的长;当点D在AB的延长线上,此时r=3,则8-$\frac{5}{8}$x=3,然后方程求出x后计算x-5即可得到AD的长.
解答 解:(1)作PF⊥BD于F,作AH⊥BC于H,如图,设⊙P的半径为r,
∵AB=AC,
∴BH=CH,
在Rt△ABH中,∵cosB=$\frac{BH}{AB}$=$\frac{4}{5}$,
∴BH=$\frac{4}{5}$×5=4,
∴AH=3,BC=2BH=8,
在Rt△ABH中,sinB=$\frac{3}{5}$
在Rt△BPH中,sinB=$\frac{PF}{PB}$=$\frac{3}{5}$,
∴PF=$\frac{3}{5}$(8-r),
当⊙P与AB相切时,PF=PC,即$\frac{3}{5}$(8-r)=r,解得r=3,
即当⊙P与AB相切时,⊙P的半径为3;
(2)∵∠BPD=∠BAC,∠DBP=∠ABC,
∴△BDP∽△BCA,
∴$\frac{BP}{BA}$=$\frac{BD}{BC}$,即$\frac{8-r}{5}$=$\frac{x}{8}$,
∴r=8-$\frac{5}{8}$x,
作PG⊥CE于G,如图,则CG=EG=$\frac{1}{2}$y,
∵PE=PC,
∴∠EPG=$\frac{1}{2}$∠EPC,
∵△BDP∽△BCA,
∴∠D=∠C=∠B,
∴PB=PD,
∴∠DPF=$\frac{1}{2}$∠DPB,
∴∠GPF=$\frac{1}{2}$∠DPC+$\frac{1}{2}$∠DPB=90°,
∴FP⊥PG,
∴∠GPC=∠B,
在Rt△PGC中,sinB=$\frac{CG}{PC}$=$\frac{3}{5}$,
∴$\frac{1}{2}$y=$\frac{3}{5}$r,
∴$\frac{1}{2}$y=$\frac{3}{5}$(8-$\frac{5}{8}$x),
∴y=$\frac{192-15x}{20}$,
当P点在C点时,r=0,即8-$\frac{5}{8}$x=0,解得x=$\frac{64}{5}$,
∴x的取值范围为5<x<$\frac{64}{5}$;
(3)∵⊙O与⊙P相交于点C、E,且⊙O经过点B,
∴点O在CE和BC的垂直平分线上,
即点O为AH和GP的交点,如图,
∵∠OPH=∠GPC,
∴cos∠OPH=$\frac{PH}{OP}$=$\frac{4}{5}$,
∴PH=$\frac{4}{5}$×$\frac{5}{4}$=1,
当点P在BH上,即点D在AB上,此时r=1+4=5,则8-$\frac{5}{8}$x=5,解得x=$\frac{24}{5}$,
∴AD=AB-AD=5-x=5-$\frac{24}{5}$=$\frac{1}{5}$
当点P在CH上,即点D在AB的延长线上,此时r=4-1=3,则8-$\frac{5}{8}$x=3,解得x=8,
∴AD=AD-AB=8-5=3,
综上所述,AD的长为$\frac{1}{5}$或3.
点评 本题考查了圆的综合题:熟练掌握等腰三角形的性质、垂径定理、三角形外心的性质和切线的性质;会利用三角函数的定义和相似三角形的性质进行几何计算;运用等腰三角形的性质构建直角三角形是解决问题的关键.

 已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )
已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )| A. | x>-2 | B. | x<-2 | C. | x>0 | D. | x<0 |
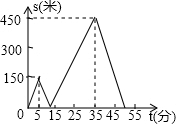 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.当甲乙两人相距360米时,求所有符合条件的t的值的和为68.5.
甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.当甲乙两人相距360米时,求所有符合条件的t的值的和为68.5. 如图是一个转盘,若转到红色则小明胜,转到黑色则小东胜,这个游戏对双方是否公平?请说明理由.
如图是一个转盘,若转到红色则小明胜,转到黑色则小东胜,这个游戏对双方是否公平?请说明理由.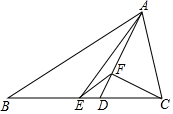 如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为3.5.
如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为3.5.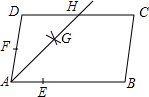 如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )