题目内容
9.甲、乙二人做某种机械零件,已知甲是技术能手每小时比乙多做3个,甲做30个所用的时间与乙做20个所用的时间相等,那么甲每小时做9个零件.分析 设甲每小时做x个零件,乙每小时做y个零件,根据题意列出关于x、y的二元一次方程组,解方程组即可得出结论.
解答 解:设甲每小时做x个零件,乙每小时做y个零件,
依题意得:$\left\{\begin{array}{l}{x=y+3}\\{\frac{30}{x}=\frac{20}{y}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=9}\\{y=6}\end{array}\right.$.
故答案为:9.
点评 本题考查了解二元一次方程组,解题的关键根据数量关系列出关于x、y的二元一次方程组.本题属于基础题,难度不大,解决该题型题目时,结合题意列出方程(或方程组)是关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
20.用科学记数法表示-0.000037,正确的是( )
| A. | 0.37×10-4 | B. | 3.7×10-4 | C. | -3.7×10-5 | D. | -3.7×10-4 |
4.对于不等式组$\left\{\begin{array}{l}{\frac{1}{2}x-1≤7-\frac{3}{2}x}\\{5x+2>3(x-1)}\end{array}\right.$下列说法正确的是( )
| A. | 此不等式组无解 | B. | 此不等式组有7个整数解 | ||
| C. | 此不等式组的负整数解是-3,-2,-1 | D. | 此不等式组的解集是-$\frac{5}{2}$<x≤2 |
14.某运动员在一场篮球比赛中的技术统计如表所示:
注:表中出手投篮次数和投中次数均不包括罚球.
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个.
| 技术 | 上场时间(分钟) | 出手投篮(次) | 投中 (次) | 罚球得分 | 篮板 (个) | 助攻(次) | 个人总得分 |
| 数据 | 46 | 66 | 22 | 10 | 11 | 8 | 60 |
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个.
19.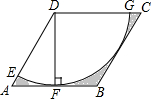 如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
 如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )| A. | 18$\sqrt{3}$-9π | B. | 18-3π | C. | 9$\sqrt{3}$-$\frac{9π}{2}$ | D. | 18$\sqrt{3}$-3π |
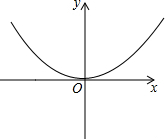 已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0,$\frac{1}{4a}$),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为$\frac{1}{8}$.
已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0,$\frac{1}{4a}$),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为$\frac{1}{8}$. 如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.