题目内容
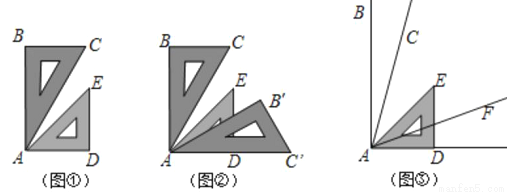
一副直角三角板(其中一个三角板的内角是45°,45°,90°,另一个是30°,60°,90°)
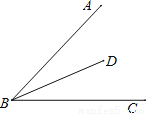
(1)如图①放置,AB⊥AD,∠CAE=_______,BC与AD的位置关系是__________;
(2)在(1)的基础上,再拿一个30°,60°,90°的直角三角板,如图②放置,将AC′边和AD边重合, AE是∠CAB′的角平分线吗,如果是,请加以说明,如果不是,请说明理由.
(3)根据(1)(2)的计算,请解决下列问题:
如图③∠BAD=90°,∠BAC=∠FAD= 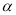 (
(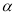 是锐角),将一个45°,45°,90°直角三角板的一直角边与AD边重合,锐角顶点A与∠BAD的顶点重合,AE是∠CAF的角平分线吗?如果是,请加以说明,如果不是,请说明理由.
是锐角),将一个45°,45°,90°直角三角板的一直角边与AD边重合,锐角顶点A与∠BAD的顶点重合,AE是∠CAF的角平分线吗?如果是,请加以说明,如果不是,请说明理由.
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目


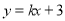 与直线
与直线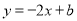 平行,则( )
平行,则( )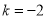 ,
, 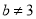 B.
B. 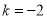 ,
, 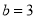 C.
C. 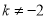 ,
, 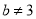 D.
D. 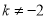 ,
, 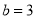
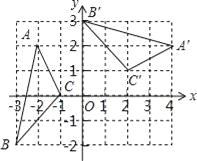
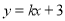 与直线
与直线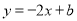 平行,则( )
平行,则( )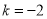 ,
, 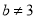 B.
B. 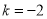 ,
, 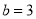 C.
C. 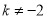 ,
, 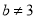 D.
D. 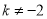 ,
, 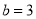
 过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点. 上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.