题目内容
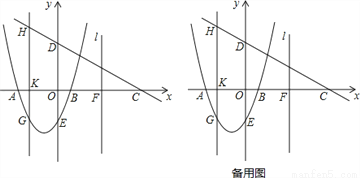
如图,抛物线y=ax2+bx-3交x轴于点A(﹣3,0),点B(1,0),交y轴于点E.点C是点A关于点B的对称点,点F是线段BC的中点,直线 过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
(1)求抛物线的函数表达式;
(2)点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于点G,求线段HG长度的最大值;
(3)在直线 上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


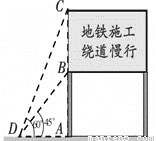
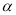 (
(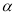 是锐角),将一个45°,45°,90°直角三角板的一直角边与AD边重合,锐角顶点A与∠BAD的顶点重合,AE是∠CAF的角平分线吗?如果是,请加以说明,如果不是,请说明理由.
是锐角),将一个45°,45°,90°直角三角板的一直角边与AD边重合,锐角顶点A与∠BAD的顶点重合,AE是∠CAF的角平分线吗?如果是,请加以说明,如果不是,请说明理由.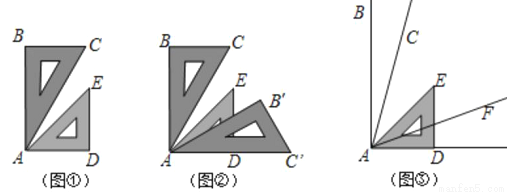
 ,N
,N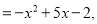 则2M-N的结果是( )
则2M-N的结果是( )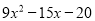 B.
B. 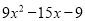 C.
C. 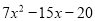 D.
D. 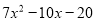
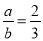 ,则
,则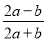 __________.
__________.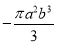 的系数和次数分别是( )
的系数和次数分别是( )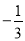 ,6 B.
,6 B. 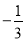 ,5 C.
,5 C. 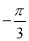 ,5 D.
,5 D. 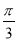 ,5
,5