题目内容
7.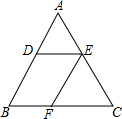 如图:在△ABC中,DE∥BC,EF∥AB,AD=3k,BD=4k,则$\frac{BF}{FC}$的值是( )
如图:在△ABC中,DE∥BC,EF∥AB,AD=3k,BD=4k,则$\frac{BF}{FC}$的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{3}$ |
分析 根据平行线分线段成比例定理求出$\frac{AD}{BD}$=$\frac{AE}{CE}$,$\frac{AE}{CE}$=$\frac{BF}{FC}$,求出$\frac{AD}{BD}$=$\frac{BF}{FC}$,把AD=3k、BD=4k代入求出即可.
解答 解:∵DE∥BC,EF∥AB,
∴$\frac{AD}{BD}$=$\frac{AE}{CE}$,$\frac{AE}{CE}$=$\frac{BF}{FC}$,
∴$\frac{AD}{BD}$=$\frac{BF}{FC}$,
∵AD=3k,BD=4k,
∴$\frac{BF}{FC}$=$\frac{3k}{4k}$=$\frac{3}{4}$.
故选A.
点评 本题考查了平行线分线段成比例定理的应用,能正确利用定理得出比例式是解此题的关键.

练习册系列答案
相关题目
15.抗震期间,某个别商贩将每件a元的食品提价20%后销售,当地政府及时采取措施,使每件食品的价格在涨价后下降15%,那么降价后每件的价格是( )元.
| A. | 1.2a | B. | 1.02a | C. | a | D. | 0.18 |

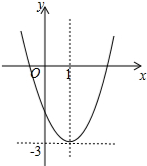 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m<-3;④3a+b>0.其中,正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m<-3;④3a+b>0.其中,正确结论的个数是( )