题目内容
2.把$\frac{-1}{3a+6}$,$\frac{2}{{a}^{2}+2a+1}$,$\frac{a}{{a}^{2}+3a+2}$通分后,各分式的分子之和为( )| A. | 2a2+7a+11 | B. | a2+8a+10 | C. | 2a2+4a+4 | D. | 4a2+11a+13 |
分析 先找出三个分式的最简公分母,再根据分式的基本性质进行解答即可.
解答 解:$\frac{-1}{3a+6}=\frac{-1}{3(a+2)}=\frac{-(a+1)^{2}}{3(a+1)^{2}(a+2)}$,
$\frac{2}{{a}^{2}+2a+1}=\frac{6(a+2)}{3(a+1)^{2}(a+2)}$,
$\frac{a}{{a}^{2}+3a+2}=\frac{3a(a+1)}{3(a+1)^{2}(a+2)}$,
所以把$\frac{-1}{3a+6}$,$\frac{2}{{a}^{2}+2a+1}$,$\frac{a}{{a}^{2}+3a+2}$通分后,
各分式的分子之和为-(a+1)2+6(a+2)+3a(a+1)=2a2+7a+11,
故选A.
点评 此题考查了通分,用到的知识点是分式的基本性质,关键是找出分式的最简公分母.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
17.某果品公司欲请汽车运输公司或火车货运站将一批水果从A地运到B地,已知汽车和火车从A地运到B地的运输路程均为x(x>0)千米,若这批水果在运输过程中(含装卸时间)的损耗都为180元/时,要收取的其他费用及有关运输资料由下表给出:
(1)请你分别用含x的代数式表示用汽车运输所需总费用M(元)和用火车运输所需总费用N(元);
(2)当A、B两地路程为600千米时,那么你认为采用哪种运输工具比较好(即运输所需总费用较少)?
| 运输工具 | 途中平均速度 (单位:千米/时) | 途中平均费用 (单位:元/千米) | 装卸时间 (单位:小时) | 装卸费用 (单位:元) |
| 汽车 | 60 | 8 | 2 | 1500 |
| 火车 | 100 | 6 | 4 | 2400 |
(2)当A、B两地路程为600千米时,那么你认为采用哪种运输工具比较好(即运输所需总费用较少)?
12.下列各式中最简分式是( )
| A. | $\frac{2a}{3ab}$ | B. | $\frac{2a}{2a-1}$ | C. | $\frac{a-1}{3a-3}$ | D. | $\frac{6{a}^{2}b}{8a}$ |
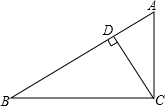 如图所示,在Rt△ACB中,∠BCA=90°,CD是斜边上的高,∠ACD=30°,AD=1,求AC,CD,BC,BD,AB的长.
如图所示,在Rt△ACB中,∠BCA=90°,CD是斜边上的高,∠ACD=30°,AD=1,求AC,CD,BC,BD,AB的长. 某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?
某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?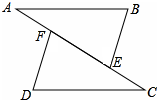 如图,点A、F、E、C在同一条直线上,AF=CE,BE=DF,AB=CD,求证:AB∥CD.
如图,点A、F、E、C在同一条直线上,AF=CE,BE=DF,AB=CD,求证:AB∥CD.