题目内容
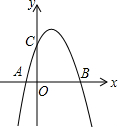 已知抛物线的表达式为y=-x2+2x+3.
已知抛物线的表达式为y=-x2+2x+3.(1)求此抛物线与x轴、y轴的交点坐标;
(2)求抛物线与坐标轴围成的三角形的面积;
(3)在上述的抛物线上是否存在这样的点P,使S△ABP=S△ABC?若存在,求出P点的坐标.
(4)在上述的抛物线上是否存在这样的点P,使S△ABP=
| 4 |
| 3 |
(5)在上述的抛物线上是否存在这样的点P,使S△ABP=
| 5 |
| 3 |
考点:抛物线与x轴的交点,二次函数图象上点的坐标特征
专题:
分析:(1)当x=0时可求得点C坐标,当y=0时可求得点A,B坐标,即可解题;
(2)根据A,B坐标可以求得AB长度,根据C点坐标可以求得OC长度,即可解题;
(3)存在,根据S△ABP=S△ABC可得点P纵坐标与点C纵坐标相等,且为3,即可求得点P坐标;
(4)存在,根据S△ABP=
S△ABC可得点P纵坐标为4,即可求得点P坐标;
(5)不存在,根据S△ABP=
S△ABC可得点P纵坐标为5,方程无解,故不存在.
(2)根据A,B坐标可以求得AB长度,根据C点坐标可以求得OC长度,即可解题;
(3)存在,根据S△ABP=S△ABC可得点P纵坐标与点C纵坐标相等,且为3,即可求得点P坐标;
(4)存在,根据S△ABP=
| 4 |
| 3 |
(5)不存在,根据S△ABP=
| 5 |
| 3 |
解答:解:(1)当x=0时,y=0+0+3=3,
∴C点坐标为(0,3),
当y=0时,0=-x2+2x+3,整理得:x2-2x-3=0,
解得:x=-1或3,
∵A点在B点左侧,
∴A(-1,0),B(3,0);
(2)∴S△ABC=
AB•OC=6;
(3)存在,
∵S△ABP=S△ABC,
∴点P纵坐标与点C纵坐标相等,且为3,
∴-x2+2x+3=3,
解得:x=2或0,∴点P坐标为(2,3);
(4)存在,
∵S△ABP=
S△ABC,
∴点P纵坐标为点C纵坐标
倍,即为4,
∴-x2+2x+3=4,
解得:x=1,∴点P坐标为(1,4);
(5)不存在,
∵S△ABP=
S△ABC,
∴点P纵坐标为点C纵坐标
倍,即为5,
∴-x2+2x+3=5,
解得:x无解,∴不存在点P.
∴C点坐标为(0,3),
当y=0时,0=-x2+2x+3,整理得:x2-2x-3=0,
解得:x=-1或3,
∵A点在B点左侧,
∴A(-1,0),B(3,0);
(2)∴S△ABC=
| 1 |
| 2 |
(3)存在,
∵S△ABP=S△ABC,
∴点P纵坐标与点C纵坐标相等,且为3,
∴-x2+2x+3=3,
解得:x=2或0,∴点P坐标为(2,3);
(4)存在,
∵S△ABP=
| 4 |
| 3 |
∴点P纵坐标为点C纵坐标
| 4 |
| 3 |
∴-x2+2x+3=4,
解得:x=1,∴点P坐标为(1,4);
(5)不存在,
∵S△ABP=
| 5 |
| 3 |
∴点P纵坐标为点C纵坐标
| 5 |
| 3 |
∴-x2+2x+3=5,
解得:x无解,∴不存在点P.
点评:本题考查了抛物线和坐标轴交点的求解,考查了抛物线上点的求解,本题中求得△ABC的面积是解题的关键.

练习册系列答案
相关题目
下列各组数中能构成直角三角形的是( )
| A、3,4,7 | ||||||
B、
| ||||||
| C、4,6,8 | ||||||
| D、9,40,41 |
已知a、b都是有理数,且(a+1)2+|b-2014|=0,则ab等于( )
| A、3 | B、-1 | C、1 | D、5 |
2014年“双十一”当天,阿里巴巴当天交易额达到惊人的571亿元,请用科学记数法表示571亿为( )
| A、5.71×108 |
| B、5.71×1010 |
| C、5.71×109 |
| D、5.71×1011 |
 如图,⊙O是直径BC,弦AB,∠BAC的平分线交⊙O于点D.
如图,⊙O是直径BC,弦AB,∠BAC的平分线交⊙O于点D.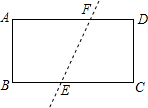 已知,如图,在矩形(两组对边平行且相等,四个内角都为直角)ABCD中,AB=4,BC=8,把它沿直线EF折叠,点C与点A重合,求CE的长.
已知,如图,在矩形(两组对边平行且相等,四个内角都为直角)ABCD中,AB=4,BC=8,把它沿直线EF折叠,点C与点A重合,求CE的长.