题目内容
如图，点D是△ABC的边BC上一点，且AB=AC，AD=AE，∠BAD=30°，则∠EDC=考点：等腰三角形的性质
专题：
分析：根据三角形的一个外角等于和它不相邻的两个内角的和，∠AED=∠EDC+∠C，∠ADC=∠B+∠BAD，再根据等边对等角的性质∠B=∠C，∠ADE=∠AED，代入数据计算即可求出∠BAD的度数．
解答：解：如图，∠AED=∠EDC+∠C，∠ADC=∠B+∠BAD，
∵AD=AE，
∴∠AED=∠ADE，
∵AB=AC，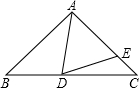
∴∠B=∠C，
∵∠ADC=∠B+∠BAD，
∴∠B+∠BAD=∠EDC+∠C+∠EDC，
即∠BAD=2∠EDC，
∵∠BAD=30°，
∴∠EDC=15°．
故答案为：15．
∵AD=AE，
∴∠AED=∠ADE，
∵AB=AC，
∴∠B=∠C，
∵∠ADC=∠B+∠BAD，
∴∠B+∠BAD=∠EDC+∠C+∠EDC，
即∠BAD=2∠EDC，
∵∠BAD=30°，
∴∠EDC=15°．
故答案为：15．
点评：此题考查的知识点是等腰三角形的性质，利用三角形的一个外角等于和它不相邻的两个内角的和的性质，熟练掌握性质是解题的关键．
练习册系列答案
相关题目
如图所示，要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和相等，则a+b+c=
如图，在菱形ABCD中，BE⊥AD，垂足为E，且E为AD为中点．则∠ADC=如果三角形三边长为5，m，n，且（m+n）（m-n）=25，那么此三角形形状为（ ）
| A、锐角三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |