题目内容
 如图,在菱形ABCD中,BE⊥AD,垂足为E,且E为AD为中点.则∠ADC=
如图,在菱形ABCD中,BE⊥AD,垂足为E,且E为AD为中点.则∠ADC=考点:菱形的性质
专题:
分析:由在菱形ABCD中,BE⊥AD,垂足为E,且E为AD为中点,易证得△ABD是等边三角形,继而求得答案.
解答:解:∵BE⊥AD,且E为AD为中点,
∴AB=BD,
∵四边形ABCD是菱形,
∴AB=AD,∠ADC=2∠ADB,
∴AB=BD=AD,
∴△ABD是等边三角形,
∴∠ADB=60°,
∴∠ADC=2∠ADB=120°.
故答案为:120.
∴AB=BD,
∵四边形ABCD是菱形,
∴AB=AD,∠ADC=2∠ADB,
∴AB=BD=AD,
∴△ABD是等边三角形,
∴∠ADB=60°,
∴∠ADC=2∠ADB=120°.
故答案为:120.
点评:此题考查了菱形的性质、等边三角形的判定与性质以及线段垂直平分线的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 如图,当半径为30cm的传送带转动轮转过120°角时,传送带上的物体A平移的距离为
如图,当半径为30cm的传送带转动轮转过120°角时,传送带上的物体A平移的距离为 如图,∠A=65°,∠B=85°,CE是∠ACD的角平分线,那么∠ECD=
如图,∠A=65°,∠B=85°,CE是∠ACD的角平分线,那么∠ECD=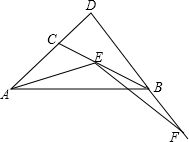 如图,△ABD中,C是AD上的一点,且AD=k•DB,DB=k•DC,AC=m•BC,E是直线BC上一点,∠AEF=∠ACB,EF交直线DB于F,试探究AE与EF之间的数量关系.
如图,△ABD中,C是AD上的一点,且AD=k•DB,DB=k•DC,AC=m•BC,E是直线BC上一点,∠AEF=∠ACB,EF交直线DB于F,试探究AE与EF之间的数量关系. 如图,点D是△ABC的边BC上一点,且AB=AC,AD=AE,∠BAD=30°,则∠EDC=
如图,点D是△ABC的边BC上一点,且AB=AC,AD=AE,∠BAD=30°,则∠EDC=