题目内容
 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.(1)求证:AE=GF;
(2)试探究四边形AEFD是什么特殊四边形?请回答并证明你的结论;
(3)设AE=5,求四边形DEGF的面积.(特别提醒:表示角最好用数字)
考点:四边形综合题
专题:
分析:(1)先根据∠C=60°,DG是梯形ABCD的高,F是CD的中点得出GF=CF.由平行线的性质得出∠BAD=120°,由AB=AD,AE⊥BD于点E可知∠DAE=
∠BAD=60°,故可得出△DGC≌△DEA,所以AE=CG,由此可得出结论;
(2)由等腰三角形的性质(三线合一),可得BE=DE,又由F是CD的中点,可得EF是△DBC的中位线,易得四边形AEFD是平行四边形;
(2)由(2)可知:EF⊥DG,所以四边形DEGF的面积=
EF•DG;根据直角三角形的性质,即可求得EF与DG的长,即可求得四边形的面积.
| 1 |
| 2 |
(2)由等腰三角形的性质(三线合一),可得BE=DE,又由F是CD的中点,可得EF是△DBC的中位线,易得四边形AEFD是平行四边形;
(2)由(2)可知:EF⊥DG,所以四边形DEGF的面积=
| 1 |
| 2 |
解答: (1)证明:∵在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,
(1)证明:∵在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,
∴梯形ABCD是等腰梯形,
∴∠ABC=∠C=60°.
∵DG是梯形ABCD的高,F是CD的中点,
∴GF=CF,
∴△CGF是等边三角形,
∴GF=CF=CG.
∵AD∥BC,
∴∠BAD=120°.
∵AB=AD,AE⊥BD于点E,
∴∠DAE=
∠BAD=60°,
在△DGC与△DEA中,
∵
,
∴△DGC≌△DEA(AAS),
∴AE=CG,即AE=GF;
(2)平行四边形.
证明:∵AB=DC,
∴梯形ABCD为等腰梯形.
∵∠C=60°,
∴∠BAD=∠ADC=120°,
又∵AB=AD,
∴∠ABD=∠ADB=30°.
∵AD∥BC,
∴∠DBC=∠ADB=30°.
∴∠BDC=90°.
由已知AE⊥BD,
∴AE∥DC.
又∵AE为等腰三角形ABD的高,
∴E是BD的中点,
∵F是DC的中点,
∴EF∥BC.
∴EF∥AD.
∴四边形AEFD是平行四边形,
(3)解:在Rt△AED中,∠ADB=30°,
∵AE=5,
∴AD=10.
在Rt△DGC中,
∵∠C=60°,DC=AD=10,
∴DG=CD•sin60°=10×
=5
.
由(1)知:在平行四边形AEFD中EF=AD=10,
又∵DG⊥BC,
∴DG⊥EF,
∴四边形DEGF的面积=
EF•DG=
×10×5
=25
.
 (1)证明:∵在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,
(1)证明:∵在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,∴梯形ABCD是等腰梯形,
∴∠ABC=∠C=60°.
∵DG是梯形ABCD的高,F是CD的中点,
∴GF=CF,
∴△CGF是等边三角形,
∴GF=CF=CG.
∵AD∥BC,
∴∠BAD=120°.
∵AB=AD,AE⊥BD于点E,
∴∠DAE=
| 1 |
| 2 |
在△DGC与△DEA中,
∵
|
∴△DGC≌△DEA(AAS),
∴AE=CG,即AE=GF;
(2)平行四边形.
证明:∵AB=DC,
∴梯形ABCD为等腰梯形.
∵∠C=60°,
∴∠BAD=∠ADC=120°,
又∵AB=AD,
∴∠ABD=∠ADB=30°.
∵AD∥BC,
∴∠DBC=∠ADB=30°.
∴∠BDC=90°.
由已知AE⊥BD,
∴AE∥DC.
又∵AE为等腰三角形ABD的高,
∴E是BD的中点,
∵F是DC的中点,
∴EF∥BC.
∴EF∥AD.
∴四边形AEFD是平行四边形,
(3)解:在Rt△AED中,∠ADB=30°,
∵AE=5,
∴AD=10.
在Rt△DGC中,
∵∠C=60°,DC=AD=10,
∴DG=CD•sin60°=10×
| ||
| 2 |
| 3 |
由(1)知:在平行四边形AEFD中EF=AD=10,
又∵DG⊥BC,
∴DG⊥EF,
∴四边形DEGF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查的是四边形综合题,涉及到等腰梯形的性质、全等三角形的判定与性质、直角三角形的性质等知识,难度适中.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
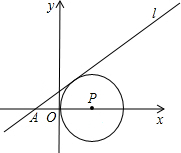 如图,点P在x轴上,OP=2,以点P为圆心,OP长为半径作圆,已知经过点A(-2,0)的直线l的函数解析式为y=kx+b,当l分别与⊙P相交、相切、相离时,求b的取值范围.
如图,点P在x轴上,OP=2,以点P为圆心,OP长为半径作圆,已知经过点A(-2,0)的直线l的函数解析式为y=kx+b,当l分别与⊙P相交、相切、相离时,求b的取值范围. 如图,△ABC中,∠A=60°,BF、CE分别是∠ABC、∠ACB的平分线,并交于点O.求证:OE=OF.
如图,△ABC中,∠A=60°,BF、CE分别是∠ABC、∠ACB的平分线,并交于点O.求证:OE=OF.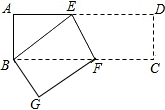 如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与D重合,已知AB=3cm,AD=9cm.
如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与D重合,已知AB=3cm,AD=9cm.