题目内容
已知圆锥的全面积为14πcm2,侧面展开图的圆心角为60°,求圆锥的体积.
考点:圆锥的计算
专题:计算题
分析:设圆锥的底面圆的半径为rcm,母线长为lcm,先根据弧长公式得到l=6r,再利用全面积得到πr2+
•2πr•l=14π,则r2+r•6r=14,解得r=
,则l=6
,接着根据勾股定理计算出圆锥的高,然后根据圆锥的体积公式计算.
| 1 |
| 2 |
| 2 |
| 2 |
解答:解:设圆锥的底面圆的半径为rcm,母线长为lcm,
根据题意得2πr=
,
所以l=6r,
又因为圆锥的全面积为14πcm2,
所以πr2+
•2πr•l=14π,
则r2+r•6r=14,解得r=
,
所以l=6
,
所以圆锥的高=
=
,
所以圆锥的体积=
•π•(
)2•
=
π.
根据题意得2πr=
| 60•π•l |
| 180 |
所以l=6r,
又因为圆锥的全面积为14πcm2,
所以πr2+
| 1 |
| 2 |
则r2+r•6r=14,解得r=
| 2 |
所以l=6
| 2 |
所以圆锥的高=
(6
|
| 70 |
所以圆锥的体积=
| 1 |
| 3 |
| 2 |
| 70 |
2
| ||
| 3 |
点评:本题考查了圆锥的计算:连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.连接顶点与底面圆心的线段叫圆锥的高;圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
 如图,△ABC≌△A′B′C,∠BCB′=40°,则∠ACA′=( )
如图,△ABC≌△A′B′C,∠BCB′=40°,则∠ACA′=( )| A、30° | B、40° |
| C、120° | D、150° |
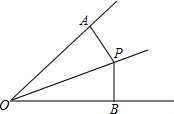 如图,点P在∠AOB的平分线上,PA⊥OA,PB⊥OB,PA=3,OB=4,则四边形AOBP的面积是
如图,点P在∠AOB的平分线上,PA⊥OA,PB⊥OB,PA=3,OB=4,则四边形AOBP的面积是 如图,△ABC中,∠A=60°,BF、CE分别是∠ABC、∠ACB的平分线,并交于点O.求证:OE=OF.
如图,△ABC中,∠A=60°,BF、CE分别是∠ABC、∠ACB的平分线,并交于点O.求证:OE=OF. 如图,在△ABC中,AD是边BC上的高,BC=AD=8,sinB=
如图,在△ABC中,AD是边BC上的高,BC=AD=8,sinB=