题目内容
如图，在菱形ABCD中，DE⊥AB，cosA=| 3 |
| 5 |
考点：菱形的性质,解直角三角形
专题：
分析：如图，设AD=5x，则AE=3x．利用菱形的性质得到BE=2x，然后利用勾股定理和解直角三角形来求tan∠BDE的值．
解答：
解：∵DE⊥AB，cosA=
，
∴
=
．
故设AD=5x，则AE=3x．
在直角△ADE中，由勾股定理得到：DE=
=4x．
∵四边形ABCD是菱形，
∴AD=AB，
∴BE=AB-AE=2x，
∴tan∠BDE=
=
．
故答案是：
．
解：∵DE⊥AB，cosA=| 3 |
| 5 |
∴
| AE |
| AD |
| 3 |
| 5 |
故设AD=5x，则AE=3x．
在直角△ADE中，由勾股定理得到：DE=
| AD2-AE2 |
∵四边形ABCD是菱形，
∴AD=AB，
∴BE=AB-AE=2x，
∴tan∠BDE=
| 2x |
| 4x |
| 1 |
| 2 |
故答案是：
| 1 |
| 2 |
点评：本题考查了菱形的性质，解直角三角形．此题利用了菱形的四条边都相等的性质．
练习册系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中有一个点A（-
，1），在坐标轴上找一个点P，使得以A、P、O为顶点的三角形是等腰三角形，则这样的点P有（ ）
| 3 |
| A、5个 | B、6个 | C、7个 | D、8个 |
如图，四边形ACED中，CE∥AD，以DC，DE为边作?DCFE，EC的延长线交AF于B，求证：AB=FB．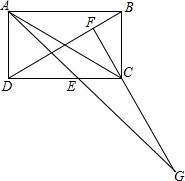
如图，矩形ABCD中，过C作CF⊥BD于F，延长FC至G，CG=BD，连AG交CD于E，∠AED的度数是多少？
如图所示，已知OA=OB，OC=OD，AD、BC相交于点E，则图中全等三角形共有（ ）| A、2对 | B、3对 | C、4对 | D、5对 |
（1）与∠E成内错角的是
试找出图中与∠1是同位角的所有角，与∠1是内错角的所有的角，与∠1是同旁内角的所有的角．如图是某几何体的三视图及相关数据，则该几何体的侧面积是（ ）
| A、acπ | ||
| B、bcπ | ||
C、
| ||
D、
|