题目内容
 将一副三角板按如图所示叠放在一起,如果阴影部分的面积为
将一副三角板按如图所示叠放在一起,如果阴影部分的面积为| 49 |
| 2 |
(7
-7)
| 3 |
(7
-7)
cm.| 3 |
分析:由FC与DE都与AE垂直,得到FC与DE平行,利用两直线平行同位角相等,得到∠AFC=∠D=45°,可得出三角形ACF为等腰直角三角形,即AC=FC,利用直角三角形的面积公式表示出三角形ACF的面积,即为阴影部分的面积,将已知的面积代入求出AC的长,即为CF的长,在直角三角形ABC中,由∠B=30°及AC的长,利用锐角三角函数定义求出BC的长,由BC-CF即可求出BF的长.
解答:解:∵BC⊥AC,DE⊥AE,
∴FC∥ED,又∠D=45°,
∴∠AFC=∠D=45°,
∴△ACF为等腰直角三角形,即AC=CF,
又∵阴影部分的面积为
cm2,即
AC•CF=
AC2=
cm2,
∴AC=CF=7cm,
在Rt△ABC中,∠B=30°,AC=7cm,
∴BC=
=7
cm,
则BF=BC-CF=(7
-7)cm.
故答案为:7
-7.
∴FC∥ED,又∠D=45°,
∴∠AFC=∠D=45°,
∴△ACF为等腰直角三角形,即AC=CF,
又∵阴影部分的面积为
| 49 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 49 |
| 2 |
∴AC=CF=7cm,
在Rt△ABC中,∠B=30°,AC=7cm,
∴BC=
| AC |
| tan30° |
| 3 |
则BF=BC-CF=(7
| 3 |
故答案为:7
| 3 |
点评:此题属于解直角三角形的题型,涉及的知识有:等腰直角三角形的判定与性质,平行线的性质,锐角三角函数定义,以及特殊角的三角函数值,其综合性较强,有利于培养同学们钻研和探索问题的精神.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
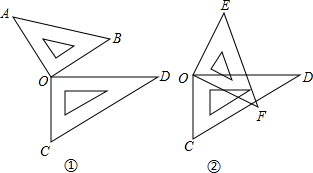
 13、将一副三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是
13、将一副三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是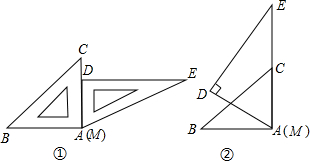
 将一副三角板按如图所示摆放在一起,连接DA,则tan∠BDA的值是
将一副三角板按如图所示摆放在一起,连接DA,则tan∠BDA的值是 (2012•聊城)将一副三角板按如图所示摆放,图中∠α的度数是( )
(2012•聊城)将一副三角板按如图所示摆放,图中∠α的度数是( )