题目内容
 将一副三角板按如图所示摆放在一起,连接DA,则tan∠BDA的值是
将一副三角板按如图所示摆放在一起,连接DA,则tan∠BDA的值是分析:先过点A作AE⊥BD于E,设AB=a,在Rt△ABC中,利用cot30°=
,可求BC,在Rt△BCD中,利用sin45°=
,又可求BD,易证△ABE是等腰直角三角形,从而利用sin45°=
,可求AE、BE,于是在Rt△ADE中,可求tan∠EDA=
=
,即tan∠BDA的值.
| 3 |
| ||
| 2 |
| ||
| 2 |
| AE |
| DE |
| AE |
| BD-BE |
解答: 解:如右图所示,过点A作AE⊥BD于E,
解:如右图所示,过点A作AE⊥BD于E,
设AB=a,
在Rt△ABC中,∠BCA=30°,那么可知
BC=cot30°×AB=
a,
在Rt△BCD中,BD=sin45°×BC=
a,
又∵AE⊥BD,∠CBD=45°,
∴BE=AE=sin45°×a=
a,
∴在Rt△ADE中,tan∠EDA=
=
=
=
.
即tan∠BDA=
.
 解:如右图所示,过点A作AE⊥BD于E,
解:如右图所示,过点A作AE⊥BD于E,设AB=a,
在Rt△ABC中,∠BCA=30°,那么可知
BC=cot30°×AB=
| 3 |
在Rt△BCD中,BD=sin45°×BC=
| ||
| 2 |
又∵AE⊥BD,∠CBD=45°,
∴BE=AE=sin45°×a=
| ||
| 2 |
∴在Rt△ADE中,tan∠EDA=
| AE |
| DE |
| AE |
| BD-BE |
| ||||||||
|
| ||
| 2 |
即tan∠BDA=
| ||
| 2 |
点评:本题考查了直角三角形的性质、特殊三角函数值.解本题最关键的是作辅助线AE,构造直角三角形.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 13、将一副三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是
13、将一副三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是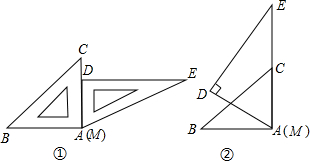
 (2012•聊城)将一副三角板按如图所示摆放,图中∠α的度数是( )
(2012•聊城)将一副三角板按如图所示摆放,图中∠α的度数是( )