Question

将一副三角板按如图①所示的位置摆放，使后两块三角板的直角边AC和MD重合，已知AB=AC=16cm，将△MED绕点A（m）逆时针旋转60°后得到图②，两个三角形重叠（阴影）部分的面积大约是多少？（结果精确到0.1cm，

3

≈1.73）

Answer 1

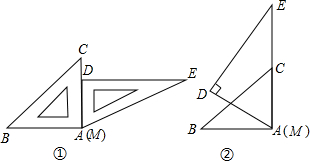
分析：过BC、AD的交点F作FG⊥AC于G，由图形可得，∠FCA=45°，∠FAG=60°，则由BG和两角的正切值表示AC的长，再求得FG的长即可，则三角形重叠（阴影）部分的面积即可求出．

解答：解：设BC、AD相交于F，过F作FG⊥AC于G．
∵∠BCA=45°，
∴CG=FG．
∵在Rt△AFG中，∠CAD=60°．
∴tan∠GAF=

FG

GA

∴GA=

3

3

FG．
设GC=xcm，
∴FG=xcm，AG=

3

3

xcm，
由CG+GA=AC得x+

3

3

x=16，
∴x=8（3-

3

）．
∴S_△AFC=

1

2

AC•FG=

1

2

×16×8（3-

3

）≈81.3（cm²）．

点评：本题考查了三角函数的应用，需学会用三角函数解直角三角形．