题目内容
 如图,直线y=-
如图,直线y=-| 3 |
| 3 |
| 3 |
(1)求点A的坐标和k的值;
(2)动点E从原点O出发,以每秒1个单位的速度沿着O-P-A的路线向点A匀速运动(E不与点O、A重合),多点E分别作EF⊥x轴于F,EB⊥y轴于B,设运动的时间为t秒.
①当点E运动在线段OP上时,若矩形EBOF的面积为3
| 3 |
②设矩形EBOF与△OPA重叠部分的面积为S,求S与t之间的函数关系式,并求S的最大值.
考点:一次函数综合题
专题:
分析:(1)由y=-
x+4
与x轴相交于点A,可得出A的坐标,由直线y=kx过点P(2,2
).代入可求得k的值.
(2))①由OE=t,可得出EF,OF的值,由矩形EBOF的面积为3
,即可解得t的值,
②当0<t≤4时,EF=
t,OF=
t,S=
EF•OF=
×
t×
t=
t2,当4<t<8时,由S=S矩形EBOF-S△AEF=EF•OF-
EF•AF求出关系式关求出最大值即可.
| 3 |
| 3 |
| 3 |
(2))①由OE=t,可得出EF,OF的值,由矩形EBOF的面积为3
| 3 |
②当0<t≤4时,EF=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 8 |
| 1 |
| 2 |
解答:解:(1)∵y=-
x+4
与x轴相交于点A,
∴A的坐标(4,0),
∵直线y=kx过点P(2,2
).
∴2
=2k,
k=
,
(2)①∵OE=t,
∴EF=
t,OF=
t,
∵矩形EBOF的面积为3
,
∴
×
t×
t=3
,解得t=2
,
②∵OP=
=4,
∴当0<t≤4时,EF=
t,OF=
t,
S=
EF•OF=
×
t×
t=
t2,
∵如图,当4<t<8时,AE=AP-(t-4)=4-(t-4)=8-t,

∴EF=
(8-t),AF=
(8-t),
∴OF=OA-AF=4-
(8-t)=
t,
在△OBM和△EFA中,
,
∴△OBM≌△EFA(HL),
∴S=S矩形EBOF-S△AEF=EF•OF-
EF•AF=
(8-t)×
t-
×
(8-t)×
(8-t)=-
(t-
)2+
,
∴S的最大值是
.
| 3 |
| 3 |
∴A的坐标(4,0),
∵直线y=kx过点P(2,2
| 3 |
∴2
| 3 |
k=
| 3 |
(2)①∵OE=t,
∴EF=
| ||
| 2 |
| 1 |
| 2 |
∵矩形EBOF的面积为3
| 3 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 6 |
②∵OP=
22+(2
|
∴当0<t≤4时,EF=
| ||
| 2 |
| 1 |
| 2 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 8 |
∵如图,当4<t<8时,AE=AP-(t-4)=4-(t-4)=8-t,

∴EF=
| ||
| 2 |
| 1 |
| 2 |
∴OF=OA-AF=4-
| 1 |
| 2 |
| 1 |
| 2 |
在△OBM和△EFA中,
|
∴△OBM≌△EFA(HL),
∴S=S矩形EBOF-S△AEF=EF•OF-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 8 |
| 16 |
| 3 |
8
| ||
| 3 |
∴S的最大值是
8
| ||
| 3 |
点评:本题主要考查了一次函数与几何图形的面积问题,解题的关键是分两种情况正确列出S与T的关系式.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
下列各组长度的线段,成比例线段的是( )
| A、2cm,4cm,4cm,8cm |
| B、2cm,4cm,6cm,8cm |
| C、1cm,2cm,3cm,4cm |
| D、2.1cm,3.1cm,4.3cm,5.2cm |
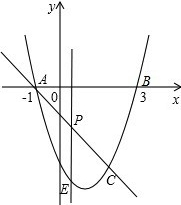 如图,抛物线y=x2+bx-3与x轴交于A、B两点(点A在点B左侧),直线l与抛物线交于A、C亮点,其中C的横坐标为2.
如图,抛物线y=x2+bx-3与x轴交于A、B两点(点A在点B左侧),直线l与抛物线交于A、C亮点,其中C的横坐标为2.