题目内容
某商场销售某种品牌的纯牛奶,已知进价为每箱40元,市场调查发现,若每箱以50元销售,平均每天可销售90箱,价格每降低1元,平均每天多售3箱,价格每升高4元,平均每天少售10箱.
(1)求出商场平均每天销售这种牛奶的利润y与每箱售价x之间的关系;
(2)每箱定价多少元时,才能使平均每天的利润最大?最大利润是多少?
(1)求出商场平均每天销售这种牛奶的利润y与每箱售价x之间的关系;
(2)每箱定价多少元时,才能使平均每天的利润最大?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)根据价格每降低1元,平均每天多售3箱,价格每升高1元,平均每天少售3箱,可得y=90-3(x-50);
(2)根据利润=销量×(售价-进价),列出利润W与x的关系式;根据求出的函数关系式,运用配方法求最大值.
(2)根据利润=销量×(售价-进价),列出利润W与x的关系式;根据求出的函数关系式,运用配方法求最大值.
解答:解:(1)由题意得,y=90-3(x-50)=240-3x(40≤x≤80);
(2)设利润为W,
则W=y(x-40)=(240-3x)(x-40)=-3x2+360x-9600(40≤x≤80);
∵-3<0,
∴W有最大值,
即当x=60时,利润W取最大值1200.
答:当售价为60元时利润最高为1200元.
(2)设利润为W,
则W=y(x-40)=(240-3x)(x-40)=-3x2+360x-9600(40≤x≤80);
∵-3<0,
∴W有最大值,
即当x=60时,利润W取最大值1200.
答:当售价为60元时利润最高为1200元.
点评:本题考查的是二次函数在实际生活中的应用,解题时首先正确理解题意,然后根据题目隐含条件列出函数关系式,然后利用二次函数的性质即可解决问题.

练习册系列答案
相关题目
下列方程中,关于x的一元二次方程是( )
| A、(x+1)2=2(x+1) | ||||
B、
| ||||
| C、ax2+bx+c=0 | ||||
| D、x2+2x=x2-1 |
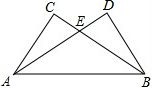 如图所示,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.
如图所示,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.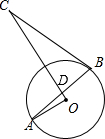 AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状.
AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状.