题目内容
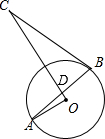 AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状.
AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状.考点:切线的性质,等腰三角形的判定
专题:常规题型
分析:连结OB,如图,根据切线的性质得OB⊥BC,则∠OBD+∠DBC=90°,再由OA⊥OD得∠A+∠ODA=90°,加上∠A=∠OBD,所以∠DBC=∠ODA,然后根据对顶角相等得到∠ODA=∠BDC,于是有∠DBC=∠BDC,最后根据等腰三角形的判定定理判断△BCD的形状.
解答:解:连结OB,如图,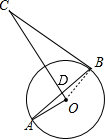
∵BC是⊙O的切线,
∴OB⊥BC,
∴∠OBD+∠DBC=90°,
∵OA⊥OD,
∴∠A+∠ODA=90°,
∵OA=OB,
∴∠A=∠OBD,
∴∠DBC=∠ODA,
而∠ODA=∠BDC,
∴∠DBC=∠BDC,
∴△BCD为等腰三角形.

∵BC是⊙O的切线,
∴OB⊥BC,
∴∠OBD+∠DBC=90°,
∵OA⊥OD,
∴∠A+∠ODA=90°,
∵OA=OB,
∴∠A=∠OBD,
∴∠DBC=∠ODA,
而∠ODA=∠BDC,
∴∠DBC=∠BDC,
∴△BCD为等腰三角形.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了等腰三角形的判定.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
计算-5+6的结果是( )
| A、-1 | B、1 | C、-5 | D、-6 |
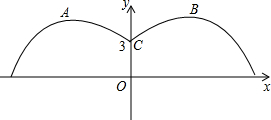 如图,一盆君子兰花的两片绿叶是形状相同的抛物线,它们的交接处距花土面3cm,两片绿叶最高点之间的距离是12cm,最高点到花土面的距离是4.2m,分别求出左、右两边抛物线的解析式.
如图,一盆君子兰花的两片绿叶是形状相同的抛物线,它们的交接处距花土面3cm,两片绿叶最高点之间的距离是12cm,最高点到花土面的距离是4.2m,分别求出左、右两边抛物线的解析式.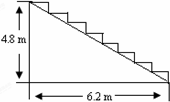 遂昌元立大酒店在重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼道宽2m,其侧面如图所示,则购买地毯至少需要
遂昌元立大酒店在重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼道宽2m,其侧面如图所示,则购买地毯至少需要