题目内容
8.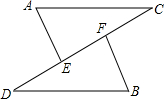 已知,如图,点E,F在CD上,DE=CF,请从下列三个条件中选择两个作为已知条件,另一个作为结论,使命题成立,并给出证明:
已知,如图,点E,F在CD上,DE=CF,请从下列三个条件中选择两个作为已知条件,另一个作为结论,使命题成立,并给出证明:①AC=BD;②∠AEC=∠BFD;③AC∥BD
我选的条件是:②③(填序号)
结论是:①(填序号)
证明:
分析 利用全等三角形的判定定理选出合适的条件和结论进行证明即可,答案不唯一.
解答 解:选择②③做条件,结论是①(答案不唯一);
证明:∵DE=CF,
∴DF=CE,
∵AC∥BD,
∴∠C=∠D,
在△AEC和△BFD中
$\left\{\begin{array}{l}{∠C=∠D}\\{DF=CE}\\{∠AEC=∠BFD}\end{array}\right.$,
∴△ABC≌△EFD(ASA),
∴AC=BD.
点评 此题主要考查了全等三角形的判定与性质以及平行线的判定,熟练掌握全等三角形的判定与性质是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.下列各式成立的是( )
| A. | -80>0.8 | B. | -2.93<-2.94 | C. | -π>-3.14 | D. | $-\frac{3}{4}$<$-\frac{2}{3}$ |
19. 数a,b在数轴上的位置如图所示,则-a-b是( )
数a,b在数轴上的位置如图所示,则-a-b是( )
 数a,b在数轴上的位置如图所示,则-a-b是( )
数a,b在数轴上的位置如图所示,则-a-b是( )| A. | 正数 | B. | 零 | C. | 负数 | D. | 都有可能 |
16.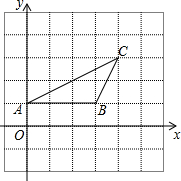 如图,在平面直角坐标系中,若△ABC三点坐标分别为A(0,1),B(3,1),C(4,3),如果要找一点D,使△ABD与△ABC全等,那么点D的坐标是(4,-1)或(-1,3)或(-1,-1).
如图,在平面直角坐标系中,若△ABC三点坐标分别为A(0,1),B(3,1),C(4,3),如果要找一点D,使△ABD与△ABC全等,那么点D的坐标是(4,-1)或(-1,3)或(-1,-1).
 如图,在平面直角坐标系中,若△ABC三点坐标分别为A(0,1),B(3,1),C(4,3),如果要找一点D,使△ABD与△ABC全等,那么点D的坐标是(4,-1)或(-1,3)或(-1,-1).
如图,在平面直角坐标系中,若△ABC三点坐标分别为A(0,1),B(3,1),C(4,3),如果要找一点D,使△ABD与△ABC全等,那么点D的坐标是(4,-1)或(-1,3)或(-1,-1).
20.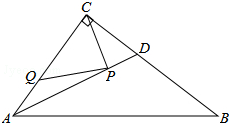 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是△ABC的角平分线,若P,Q分别是AD和AC边上的动点,则PC+PQ的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是△ABC的角平分线,若P,Q分别是AD和AC边上的动点,则PC+PQ的最小值是( )
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是△ABC的角平分线,若P,Q分别是AD和AC边上的动点,则PC+PQ的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是△ABC的角平分线,若P,Q分别是AD和AC边上的动点,则PC+PQ的最小值是( )| A. | $\frac{6}{5}$ | B. | 2 | C. | $\frac{12}{5}$ | D. | $\frac{5}{2}$ |
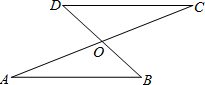 已知,如图,AC和BD相交于点O,OA=OC,OB=OD,求证:AB∥CD.
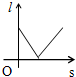
已知,如图,AC和BD相交于点O,OA=OC,OB=OD,求证:AB∥CD. 在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上,他行走在这条路上,如图,当他从A点走到B点的过程,他在灯光照射下的影长l与所走路程s的变化关系图象大致是( )
在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上,他行走在这条路上,如图,当他从A点走到B点的过程,他在灯光照射下的影长l与所走路程s的变化关系图象大致是( )