题目内容
函数y=
(a、b、k都是常数,且k≠ab)叫做“奇特函数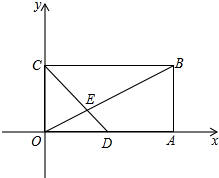 ”,当a=b=0时,奇特函数y=
”,当a=b=0时,奇特函数y=
就成为反比例函数y=
(k是常数,且k≠0).
(1)若矩形的两边长分别是2cm、3cm,当两边长分别增加xcm、ycm后得到的新矩形的面积是8cm2,求y与x的函数关系式,并判断这个函数是否“奇特函数”;
(2)如图在直角坐标系中,点O为原点矩形OABC的顶点,A、C坐标分别为(9,0)、(0,3),点D是OA中点,连接OB、CD交于E,“奇特函数”y=
的图象经过点B、E,求这个函数的解析式,并判断A、C、D三点是否在这个函数图象上;
(3)对于(2)中的“奇特函数”y=
的图象,能否经过适当的变换后与一个反比例函数图象重合,若能,请直接写出具体的变换过程和这个反比例函数解析式;若不能,请简述理由.
| ax+k |
| x+b |
 ”,当a=b=0时,奇特函数y=
”,当a=b=0时,奇特函数y=| ax+k |
| x+b |
| k |
| x |
(1)若矩形的两边长分别是2cm、3cm,当两边长分别增加xcm、ycm后得到的新矩形的面积是8cm2,求y与x的函数关系式,并判断这个函数是否“奇特函数”;
(2)如图在直角坐标系中,点O为原点矩形OABC的顶点,A、C坐标分别为(9,0)、(0,3),点D是OA中点,连接OB、CD交于E,“奇特函数”y=
| ax+k |
| x-6 |
(3)对于(2)中的“奇特函数”y=
| ax+k |
| x-6 |
考点:反比例函数综合题
专题:
分析:(1)根据矩形的面积公式,可得函数解析式,根据分式的加减,可得答案;
(2)根据图象的交点,可得E点坐标,根据待定系数法,可得奇特函数解析式,把A、C、D点的坐标代入这个函数的解析式判断即可;
(3)把y=
变形为y=
+2,即可得出向左平移6个单位长度,向下平移2个单位长度,得到反比例函数y=
.
(2)根据图象的交点,可得E点坐标,根据待定系数法,可得奇特函数解析式,把A、C、D点的坐标代入这个函数的解析式判断即可;
(3)把y=
| 2x-9 |
| x-6 |
| 3 |
| x-6 |
| 3 |
| x |
解答:解:(1)由题意得:(2+x)(3+y)=8,
∵x+2≠0,
∴3+y=
,
∴y=
-3=
,
根据新定义判断得出这个函数是“奇特函数”;
(2)由题意得:点B的坐标是(9,3),
设直线OB解析式为y=k1x,则3=9k,k=
,
直线OB解析式为y=
x,
∵点D是OA中点,
∴点D的坐标是(
,0),
设直线CD解析式为y=k2x+b,
则
,
解得:k=-
直线CD解析式为y=-
x+3,
由
得:
,
则点E的坐标是(3,1),
将B(9,3),E(3,1)代入函数y=
得:
,
解得:
,
则“奇特函数”的解析式为y=
,
∵把A点的坐标(9,0)代入得:y=
≠0,∴A点不在这个函数图象上,
∵把C点的坐标(0,3)代入得:y=
≠3,∴C点不在这个函数图象上,
∵把D点的坐标(
,0)代入得:y=
=0,∴D点在这个函数图象上;
(3)∵y=
=
=
+2,
∴向左平移6个单位长度,向下平移2个单位长度,得到反比例函数y=
.
∵x+2≠0,
∴3+y=
| 8 |
| x+2 |
∴y=
| 8 |
| x+2 |
| -3x+2 |
| x+2 |
根据新定义判断得出这个函数是“奇特函数”;
(2)由题意得:点B的坐标是(9,3),
设直线OB解析式为y=k1x,则3=9k,k=
| 1 |
| 3 |
直线OB解析式为y=
| 1 |
| 3 |
∵点D是OA中点,
∴点D的坐标是(
| 9 |
| 2 |
设直线CD解析式为y=k2x+b,
则
|
解得:k=-
| 2 |
| 3 |
直线CD解析式为y=-
| 2 |
| 3 |
由
|
|
则点E的坐标是(3,1),
将B(9,3),E(3,1)代入函数y=
| ax+k |
| x-6 |
|
解得:
|
则“奇特函数”的解析式为y=
| 2x-9 |
| x-6 |
∵把A点的坐标(9,0)代入得:y=
| 2×9-9 |
| 9-6 |
∵把C点的坐标(0,3)代入得:y=
| 2×0-9 |
| 9-6 |
∵把D点的坐标(
| 9 |
| 2 |
2×
| ||
|
(3)∵y=
| 2x-9 |
| x-6 |
| 2x-12+3 |
| x-6 |
| 3 |
| x-6 |
∴向左平移6个单位长度,向下平移2个单位长度,得到反比例函数y=
| 3 |
| x |
点评:本题考查了反比例函数综合,用到的知识点是反比例函数的图象和性质、待定系数法求函数的解析式式、函数图象的交点的求法、函数的图象平移的方法,关键是理解有关概念,求出函数的解析式.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
方程x2=x的解是( )
| A、x=1 | B、x=0 |
| C、x=±1 | D、x=1或0 |
甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.如果设甲每小时做x个零件,那么下面所列方程中正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
代数式-2x,5,3x-y,x2y,
中,单项式的个数有( )
| x+y |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
不论a,b为任何实数,a2+b2-6a+10b+35的值总是( )
| A、非负数 | B、恒为正数 |
| C、恒为负数 | D、不等于0 |
如果|x-3|+(y+2)2=0,那么x-y的值为( )
| A、1 | B、-1 | C、0 | D、5 |
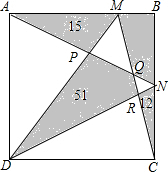 四边形ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积是多少?
四边形ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积是多少?