题目内容
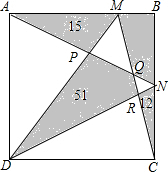四边形ABCD是一个正方形，其中几块阴影部分的面积如图所示，则四边形BMQN的面积是多少？考点：面积及等积变换
专题：计算题
分析：设正方形的边长为a，则有AB=BC=CD=AD=a，易得S△ABN+S△DCN=S△MDC，进而可得S△APM+S四边形BMQN+S△RCN=S四边形PDRQ，然后根据条件就可解决问题．
解答：解：设正方形的边长为a，则有AB=BC=CD=AD=a．
∵S△ABN+S△DCN=
BN•a+
CN•a=
a2，S△MDC=
a2，
∴S△ABN+S△DCN=S△MDC，
∴S△APM+S△MPQ+S四边形BMQN+S△DRC+S△RCN=S△MPQ+S四边形PDRQ+S△DRC，
∴S△APM+S四边形BMQN+S△RCN=S四边形PDRQ．
∵S△APM=15，S△RCN=12，S四边形PDRQ=51，
∴15+S四边形BMQN+12=51，
∴S四边形BMQN=24．
则四边形BMQN的面积是24．
∵S△ABN+S△DCN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABN+S△DCN=S△MDC，
∴S△APM+S△MPQ+S四边形BMQN+S△DRC+S△RCN=S△MPQ+S四边形PDRQ+S△DRC，
∴S△APM+S四边形BMQN+S△RCN=S四边形PDRQ．
∵S△APM=15，S△RCN=12，S四边形PDRQ=51，
∴15+S四边形BMQN+12=51，
∴S四边形BMQN=24．
则四边形BMQN的面积是24．
点评：本题主要考查了等积变换，证到S△ABN+S△DCN=S△MDC，进而得到S△APM+S四边形BMQN+S△RCN=S四边形PDRQ是解决本题的关键．
练习册系列答案
相关题目
满足下列条件的△ABC，不是直角三角形的是（ ）
| A、∠C=∠A+∠B |
| B、a：b：c=3：4：5 |
| C、∠C=∠A-∠B |
| D、∠A：∠B：∠C=3：4：5 |
”，当a=b=0时，奇特函数y=