题目内容
15. 如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.(1)求证:AF=DE;
(2)连接AD,试判断△OAD的形状,并说明理由.
分析 (1)由BE=CF,得到BF=CE,再由已知的两对角相等,利用AAS得出三角形ABF与三角形DCE全等,然后根据全等三角形的性质即可得到结论;
(2)利用全等三角形的对应角相等得到一对角相等,再利用等角对等边得到OE=OF,由于AF=DE,即可确定出三角形AOD为等腰三角形.
解答 (1)证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE,
在△ABF和△DCE中,
$\left\{\begin{array}{l}∠A=∠D\\∠B=∠C\\ BF=CE\end{array}\right.$,
∴△ABF≌△DCE,
∴AF=DE;
(2)等腰三角形,
理由:解:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴AF-OF=DE-OE,
∴OA=OD,
∴△OAD为等腰三角形.
点评 此题考查了全等三角形的判定与性质,以及等腰三角形的判定,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列各组数中,能构成三角形的是( )
| A. | 1,2,4 | B. | 4,5,9 | C. | 4,6,8 | D. | 12,5,5 |
3.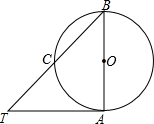 如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
 如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ①②④ |
10.下列分式变形中,正确的是( )
| A. | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | B. | $\frac{-x+y}{x+y}$=-1 | C. | $\frac{(n-m)^{3}}{(m-n)^{2}}$=n-m | D. | $\frac{a}{b}$=$\frac{am}{bm}$ |
20. 如图,在△ABC中,AB=AC,点D在AC边的右侧,连接DA、DB、DC,若AD=DC,∠ADB=∠ACB,AD=5,BD=11,则BC边的长为$\frac{24}{5}$$\sqrt{5}$.
如图,在△ABC中,AB=AC,点D在AC边的右侧,连接DA、DB、DC,若AD=DC,∠ADB=∠ACB,AD=5,BD=11,则BC边的长为$\frac{24}{5}$$\sqrt{5}$.
 如图,在△ABC中,AB=AC,点D在AC边的右侧,连接DA、DB、DC,若AD=DC,∠ADB=∠ACB,AD=5,BD=11,则BC边的长为$\frac{24}{5}$$\sqrt{5}$.
如图,在△ABC中,AB=AC,点D在AC边的右侧,连接DA、DB、DC,若AD=DC,∠ADB=∠ACB,AD=5,BD=11,则BC边的长为$\frac{24}{5}$$\sqrt{5}$.
7.直线y=2x-2向下平移4个单位得到的直线解析式是 ( )
| A. | y=2x+2 | B. | y=2x-6 | C. | y=2x-4 | D. | y=2(x+3) |
4.下列变形是属于移项的是( )
| A. | 由2x=2,得x=1 | B. | 由$\frac{x}{2}$=-1,得x=-2 | ||
| C. | 由3x-$\frac{7}{2}$=0,得3x=$\frac{7}{2}$ | D. | 由-2x-2=0,得x=-1 |