题目内容
15.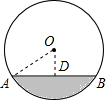 如图,小明郑处的铅球在场地上砸出一个小坑,小坑的直径AB为10cm,深为2cm(小坑的最大深度为2cm),则该铅球的半径OA为$\frac{29}{4}$cm.
如图,小明郑处的铅球在场地上砸出一个小坑,小坑的直径AB为10cm,深为2cm(小坑的最大深度为2cm),则该铅球的半径OA为$\frac{29}{4}$cm.
分析 先根据垂径定理求出AD的长,设OA=rcm,则OD=(r-2)cm,再根据勾股定理求出r的值即可.
解答 解:∵AB=10cm,OD⊥AB,小坑的最大深度为2cm,
∴AD=$\frac{1}{2}$AB=5cm.
设OA=rcm,则OD=(r-2)cm
在Rt△OAD中,
∵OA2=OD2+AD2,即r2=(r-2)2+52,
解得r=$\frac{29}{4}$cm.
故答案为$\frac{29}{4}$.
点评 本题考查的是垂径定理的应用,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
5.观察下列图形的构成规律,按此规律,第20个图形中棋子的个数是( )


| A. | 114 | B. | 214 | C. | 424 | D. | 444 |
3.下列四个数中,最小的数是( )
| A. | 0 | B. | 1 | C. | -$\frac{1}{2}$ | D. | -1 |
7.用48m长的篱笆在空地上围成一个正六边形的绿化场地,那么这个场地的面积为( )
| A. | 16$\sqrt{3}$m2 | B. | 32$\sqrt{3}$m2 | C. | $\sqrt{3}$m2 | D. | 96$\sqrt{3}$m2 |
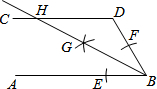 如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为32度.
如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为32度.
 已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.
已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.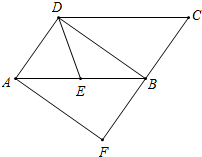 如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.
如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.