题目内容
一个三位数,将它的三个数字的排列顺序倒过来(如364写成463),所得的新三位数与原三位数之差是9的倍数吗?是11的倍数吗?为什么?
考点:整式的加减
专题:
分析:设这个三位数是100c+10b+a,则新三位数100a+10b+c,得出100a+10b+c-(100c+10b+a)=99a-99c=99(a-c),即可得出新三位数与原三位数之差是9的倍数,是11的倍数.
解答:解:是.
理由如下:
设这个三位数是100c+10b+a,则新三位数100a+10b+c,
100a+10b+c-(100c+10b+a)=99a-99c=99(a-c),
所以所得的新三位数与原三位数之差是9的倍数,是11的倍数.
理由如下:
设这个三位数是100c+10b+a,则新三位数100a+10b+c,
100a+10b+c-(100c+10b+a)=99a-99c=99(a-c),
所以所得的新三位数与原三位数之差是9的倍数,是11的倍数.
点评:本题主要考查了整式的加减,解题的关键是正确的表示出这个三位数及新三位数.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
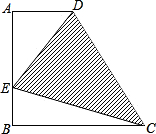 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=x,AB=BC=2x,在线段AB上有一点E,∠DCE=45°,求tan∠DEC.
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=x,AB=BC=2x,在线段AB上有一点E,∠DCE=45°,求tan∠DEC. 如图,AB是⊙O的直径,AC为弦,P为AC延长线上一点,且AC=PC,PB的延长线交⊙O于D,试说明:AC=DC.
如图,AB是⊙O的直径,AC为弦,P为AC延长线上一点,且AC=PC,PB的延长线交⊙O于D,试说明:AC=DC. 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是